
����Ŀ�������Ѿ�֪��һЩ����Ĺ����������������������еĹ�������3��4��5������������ż���еĹ�����6��8��10����ʵ�ϣ�������������������Ȼ�ǹ�������
(1)��������һЩ���ɹ������Ĺ�ʽҲ����д������������ϴ����˹ѧ������Ĺ�ʽ��a��2n+1��b��2n2+2n��c��2n2+2n+1(nΪ������)��һ�鹴��������֤���������Ϲ�ʽ��a��b��c������һ�鹴������
(2)Ȼ���������ϵ�һ�θ����Ĺ�������ʽ���ռ����ҹ��Ŵ���������ѧ�����������������У������ᵽ����a��![]() (m2��n2)��b��mn��c��
(m2��n2)��b��mn��c��![]() (m2+n2)(m��nΪ��������m��nʱ��a��b��c����һ�鹴�����������������ۣ�����������⣺��֪ijֱ�������εı߳���������������������һ�߳�Ϊ37����n��5�����ֱ�������������ߵij���
(m2+n2)(m��nΪ��������m��nʱ��a��b��c����һ�鹴�����������������ۣ�����������⣺��֪ijֱ�������εı߳���������������������һ�߳�Ϊ37����n��5�����ֱ�������������ߵij���
���𰸡�(1)֤����������(2)��n��5ʱ��һ�߳�Ϊ37��ֱ�������������ߵij��ֱ�Ϊ12��35��
��������
��1����������ֻ��Ҫ֤��a2+b2��c2�����ɽ��
��2���������⽫n��5����õ�a��![]() (m2��52)��b��5m��c��
(m2��52)��b��5m��c��![]() (m2+25)���ٽ�ֱ�������ε�һ�߳�Ϊ37���ֱ�������������a��
(m2+25)���ٽ�ֱ�������ε�һ�߳�Ϊ37���ֱ�������������a��![]() (m2��52)��b��5m��c��
(m2��52)��b��5m��c��![]() (m2+25)�����ɽ��
(m2+25)�����ɽ��
(1)��a2+b2��(2n+1)2+(2n2+2n)2��4n2+4n+1+4n4+8n3+4n2��4n4+8n3+8n2+4n+1��
c2��(2n2+2n+1)2��4n4+8n3+8n2+4n+1��
��a2+b2��c2��
��n��������
��a��b��c��һ�鹴������
(2)�⣺��n��5
��a��![]() (m2��52)��b��5m��c��
(m2��52)��b��5m��c��![]() (m2+25)��
(m2+25)��
��ֱ�������ε�һ�߳�Ϊ37��
�������������ۣ�
�ٵ�a��37ʱ��![]() (m2��52)��37��
(m2��52)��37��
���m����3![]() (�������⣬��ȥ)
(�������⣬��ȥ)
�ڵ�y��37ʱ��5m��37��
���m��![]() (����������ȥ)��
(����������ȥ)��
�۵�z��37ʱ��37��![]() (m2+n2)��
(m2+n2)��
���m����7��
��m��n��0��m��n�ǻ��ʵ�������
��m��7��
��m��7����٢ڵã�x��12��y��35��
������������n��5ʱ��һ�߳�Ϊ37��ֱ�������������ߵij��ֱ�Ϊ12��35��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��ABCD�ĶԽ���AC��BD�ཻ�ڵ�O����BDC��45��������B��BH��DC��DC���ӳ����ڵ�H����DC��ȡDE��CH���ӳ�BH��F��ʹFH��CH������DF��EF��

��1����AB��2��AD��![]() ����BH��ֵ��
����BH��ֵ��
��2����֤��AC��![]() EF��
EF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣�����ABC�У���ABΪֱ���ġ�O��AC�ڵ�D����E��BC�ϣ�����BD��DE����CDE����ABD��
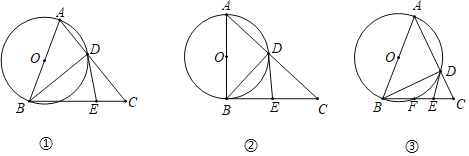
��1����֤��DE�ǡ�O�����ߣ�
��2����ͼ�ڣ�����ABC��90��ʱ���߶�DE��BC��ʲô������ϵ����˵�����ɣ�
��3����ͼ�ۣ���AB��AC��10��sin��CDE��![]() ����BC�ij���
����BC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ������ABCD��AD��BC���ֽ������²������Ե�BΪԲ�ģ��ʵ���Ϊ�뾶�������ֱ�BA��BC�ڵ�G��H���ٷֱ��Ե�G��HΪԲ�ģ�����![]() GH�ij�Ϊ�뾶��������������ABC�ڲ��ཻ�ڵ�O��������BO����AD�ڵ�E��
GH�ij�Ϊ�뾶��������������ABC�ڲ��ཻ�ڵ�O��������BO����AD�ڵ�E��
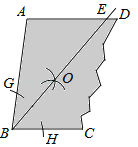
��1����֤��AB=AE��
��2������A=100��������EBC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���̳�����2�·�Ӫҵ��Ϊ400��Ԫ��3�·ݵ�Ӫҵ���2�·�����10%��5�·ݵ�Ӫҵ��ﵽ633.6��Ԫ�������̳�3�·ݵ�5�·�Ӫҵ�����ƽ��������Ϊx���������г��ķ�������ȷ���ǣ�������
A.633.6��1+x��2=400��1+10%��B.633.6��1+2x��2=400����1010%��
C.400����1+10%����1+2x��2=633.6D.400����1+10%����1+x��2=633.6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ţ�1������֯�༶�����ᣬ������齱���ڣ�ÿ��ͬѧ����һ�γ齱���ᣬ�齱�������£���һ���˿����е���Ϊ��2������3������3������5������6���������Ʊ��泯��ϴ�ȣ��ȴ��г��1���ƣ��ٴ����µ�4�����г��1���ƣ���¼�����Ƶ�����Żأ����һ�γ齱����ÿ�γ�������Ƶ���֮��Ϊ![]() ��������Ҫ��ȷ�����
��������Ҫ��ȷ�����

��1�����б�����״ͼ�ķ��������ͬѧ���һ�Ƚ��ĸ��ʣ�
��2���Ƿ�ÿ�γ齱�����Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijƷ���ֻ����۹�˾��Ӫ��Ա14�ˣ����۲�Ϊ�ƶ�Ӫ����Ա�������ֻ����ͳ������14��ij�µ����������£���λ��̨����
������ | 200 | 170 | 165 | 80 | 50 | 40 |
�� �� | 1 | 1 | 2 | 5 | 3 | 2 |
��1������14λӪ��Ա�������۸�Ʒ���ֻ���ƽ��������λ����������
��2�����۲�������ÿλӪ��Ա����������Ϊ100̨������Ϊ�Ƿ������Ϊʲô?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ���ϣ�Rt��ABC��ֱ��ΪCE�İ�ԲO��ͼ1�ڷţ���B=90�㣬AC=2CE=m��BC=n����ԲO��BC���ڵ�D������ԲO�Ƶ�C����ʱ�뷽����ת����D���ԲO��ת�ҡ�ECDʼ�յ��ڡ�ACB����ת�Ǽ�Ϊ����0��������180�㣩
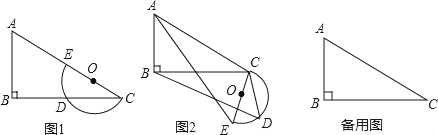
��1������=0��ʱ������DE�����CDE=�� ���㣬CD=�� ����
��2�����жϣ���ת������![]() �Ĵ�С���ޱ仯�������ͼ2�����θ���֤����
�Ĵ�С���ޱ仯�������ͼ2�����θ���֤����
��3����m=10��n=8������=��ACBʱ�����߶�BD�ij���
��4����m=6��n=4![]() ������ԲO��ת�����ABC�ı�����ʱ��ֱ��д���߶�BD�ij���
������ԲO��ת�����ABC�ı�����ʱ��ֱ��д���߶�BD�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com