
【题目】菱形ABCD中,AB=4,∠ABC=60°,∠EAF的两边分别与射线CB、DC相交于点E、F,且∠EAF=60°
(1)如图1,当点E是CB上任意一点时(点E不与B、C重合),求证:BE=CF;
(2)如图2,当点E在CB的延长线上时,且∠EAB=15°,求点F到BC的距离.

【答案】(1)证明见解析;(2)点F到BC的距离为3![]() .
.
【解析】
(1)连接AC,根据题意分析得出∠BAE=∠CAF,AB=AC,∠B=∠ACF,最后通过求出△BAE△CAF来证明结论即可;
(2)过点A作AG⊥BC于点G,过点F作FH⊥EC于点H,利用直角三角形性质求出AG、BG的长由此进一步得出BE的长,最后在Rt△CHF中利用三角函数进一步求出FH的长即可求出答案.
(1)证明:如图1,连接AC,
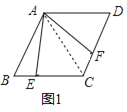
∵四边形ABCD为菱形,
∴AB=BC,AB∥CD,
∵∠ABC=60°,
∴△ABC为等边三角形,
∴AB=AC,∠BAC=60°,
∵AB∥CD,
∴∠BAC=∠ACD=60°,
∴∠B=∠ACF,
又∵∠BAC=∠EAF=60°,
∴∠BAE=∠CAF,
在△BAE和△CAF中,
∵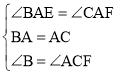 ,
,
∴△BAE△CAF,
∴BE=CF;
(2)如图2,过点A作AG⊥BC于点G,过点F作FH⊥EC于点H,
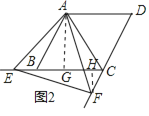
∵∠EAB=15°,∠ABC=60°,
∴∠AEB=45°,
在Rt△AGB中,
∵∠ABC=60°,AB=4,
∴BG=![]() AB=2,AG=
AB=2,AG=![]() BG=2
BG=2![]() ,
,
在Rt△AEG中,
∵∠AEG=∠EAG=45°,
∴AG=GE=2![]() ,
,
∴EB=EGBG=2![]() 2,
2,
∵四边形ABCD为菱形,
∴AB∥CD,AB=BC,
∴∠ABC=∠ECF=60°,
在△ABC中,AB=BC,∠ABC=60°,
∴△ABC为等边三角形,
∴AB=AC,∠ACB=∠BAC=60°,
∴∠ACF=∠ACB+∠ECF=120°,
∵∠ABC=60°,
∴∠ABE=120°,
∴∠ACF=∠ABE,
∵∠EAF=∠EAB+∠BAF=60°,∠BAC=∠CAF+∠BAF=60°,
∴∠EAB=∠FAC,
在△AEB与△AFC中,
∵∠EAB=∠FAC,AB=AC,∠ABE=∠ACF,
∴△AEB△AFC,
∴AE=AF,EB=CF=2![]() 2,
2,
在Rt△CHF中,∵∠HCF=180°﹣∠BCD=60°,CF=2![]() 2,
2,
∴FH=CFsin60°=(2![]() 2)
2)![]() =3
=3![]() .
.
∴点F到BC的距离为3![]() .
.


科目:初中数学 来源: 题型:
【题目】太阳能是来自太阳的辐射能量,对于地球上的人类来说,太阳能是对环境无任何污染的可再生能源,因此许多国家都在大陆发展太阳能.如图是2013-2017年我国光伏发电装机容量统计图.根据统计图提供的信息,判断下列说法不合理的是( )
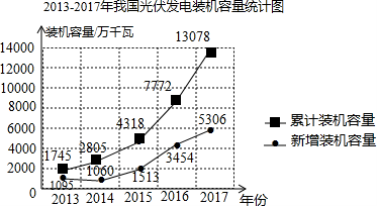
A.截至2017年底,我国光伏发电累计装机容量为13078万千瓦
B.2013-2017年,我国光伏发电新增装机容量逐年增加
C.2013-2017年,我国光伏发电新增装机容量的平均值约为2500万千瓦
D.2017年我国光伏发电新增装机容量大约占当年累计装机容量的40%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红参加学校组织的庆祝党的十九大胜利召开知识竞赛,答对最后两道单选题就顺利通关,第一道单选题有3个选项,第二道单选题有4个选项,可是小红这两道题都不会,不过竞赛规则规定每位选手有两次求助机会,使用“求助”一次可以让主持人去掉其中一题的一个错误选项,主持人提醒小红可以使用两次“求助”.
(1)如果小红两次“求助”都在第一道题中使用,那么小红通关的概率是 .
(2)如果小红将每道题各用一次“求助”,请用树状图或者列表来分析她顺序通关的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() .
.
(1)尺规作图:以![]() 为直径作
为直径作![]() ,分别交
,分别交![]() 和
和![]() 于点
于点![]() 和
和![]() .(保留作图痕迹,不写做法)
.(保留作图痕迹,不写做法)
(2)过![]() 作
作![]() ,垂足为
,垂足为![]()
①求证:![]() 为
为![]() 的切线.
的切线.
②连接![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的半径长.
的半径长.

查看答案和解析>>
科目:初中数学 来源: 题型:
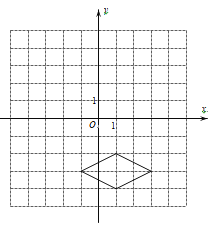
【题目】在平面直角坐标系中,x轴下方有一个菱形,如图所示,画图并回答问题.
(1)将x轴下方的菱形先向右平移2个单位长度,再向上平移6个单位长度,画出平移后的图形;
(2)将x轴下方的菱形绕着原点顺时针方向旋转 90°,画出旋转后的图形;
(3)在(1)和(2)中画出的两个图形存在一种特殊关系,即一个图形绕着某点旋转一个角度可以得到另一个图形,请直接写出旋转中心的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=45°,将△ABC绕点A逆时针方向旋转得△AEF,其中,E,F是点B,C旋转后的对应点,BE,CF相交于点D.若四边形ABDF为菱形,则∠CAE的大小是( )
![]()
A. 45°B. 60°C. 75°D. 90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=4,以BC为直径的半圆O交斜边AB于点 D.
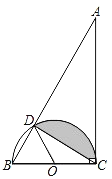
(1)证明:AD=3BD;
(2)求弧BD的长度;
(3)求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A、B两地同时出发,在同一条公路上,匀速行驶,相向而行,到两车相遇时停止.甲车行驶一段时间后,因故停车0.5小时,故障解除后,继续以原速向B地行驶,两车之间的路程y(千米)与出发后所用时间x(小时)之间的函数关系如图所示.

(1)求甲、乙两车行驶的速度V甲、V乙.
(2)求m的值.
(3)若甲车没有故障停车,求可以提前多长时间两车相遇.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com