
【题目】如图,在![]() 中,
中,![]() .
.
(1)尺规作图:以![]() 为直径作
为直径作![]() ,分别交
,分别交![]() 和
和![]() 于点
于点![]() 和
和![]() .(保留作图痕迹,不写做法)
.(保留作图痕迹,不写做法)
(2)过![]() 作
作![]() ,垂足为
,垂足为![]()
①求证:![]() 为
为![]() 的切线.
的切线.
②连接![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的半径长.
的半径长.

【答案】(1)画图见解析;(2)①证明见解析,②2.
【解析】
(1)根据题意,以![]() 为直径作
为直径作![]() ,分别交
,分别交![]() 和
和![]() 于点
于点![]() 和
和![]() 作图即可.
作图即可.
(2)①作AB的中点O,连接OE、AE,根据等腰三角形的性质可得![]() ,再根据圆周角定理可得
,再根据圆周角定理可得![]() ,即可得
,即可得![]() ,
,![]() ,再根据余角的性质可得
,再根据余角的性质可得![]() ,再根据等腰三角形的性质可得
,再根据等腰三角形的性质可得![]() ,从而得出
,从而得出![]() ,即可得证
,即可得证![]() 为
为![]() 的切线.②过点O作
的切线.②过点O作![]() ,根据垂径定理得到D为AF的中点,设圆的半径为r,表示出AF,AD以及HD,在直角三角形OAD中,表示出OD2,在直角三角形ODH中,利用勾股定理列出关于r的方程,求出方程的解即可.
,根据垂径定理得到D为AF的中点,设圆的半径为r,表示出AF,AD以及HD,在直角三角形OAD中,表示出OD2,在直角三角形ODH中,利用勾股定理列出关于r的方程,求出方程的解即可.
(1)如图所示,即为所求.
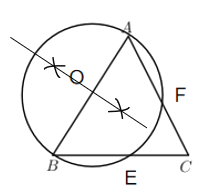
(2)①作AB的中点O,连接OE、AE
∵![]()
∴![]()
∵AB是![]() 的直径
的直径
∴![]()
∴![]() ,
,![]()
∵![]()
∴![]()
∴![]()
∴![]()
∵OA、OE是圆的半径
∴![]()
∴![]()
∴![]()
∴![]() 为
为![]() 的切线
的切线
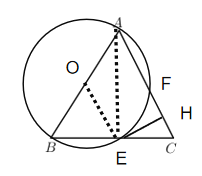
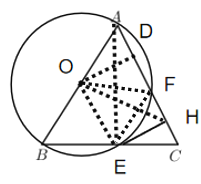
②连接![]() ,过点O作
,过点O作![]()
∵AB是圆O的直径
![]()
![]()
![]()
![]()
∵EH是圆O的切线
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
∴![]()
∵OA、OF为圆的半径
∴![]()
∵![]()
∴![]()
设圆的半径为r,则![]()
∴![]()
∴![]()
在Rt△AOD中,根据勾股定理得
![]()
在Rt△ODH中,根据勾股定理得
![]()
即![]()
解得![]() (舍去)或
(舍去)或![]()
则圆的半径为2.


科目:初中数学 来源: 题型:
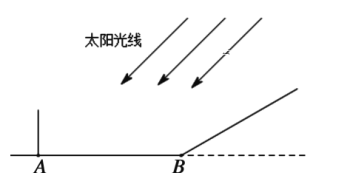
【题目】小芳身高1.6米,此时太阳光线与地面的夹角为45°.
(1)若小芳正站在水平地面A处上时,那么她的影长为多少米?
(2)若小芳来到一个坡度i=![]() 的坡面底端B处,当她在坡面上至少前进多少米时,小芳的影子恰好都落在坡面上?
的坡面底端B处,当她在坡面上至少前进多少米时,小芳的影子恰好都落在坡面上?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,把点
中,把点![]() 沿
沿![]() 对折,使点
对折,使点![]() 落在
落在![]() 上的
上的![]() 点,已知
点,已知![]() ,
,![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)如果一条不与抛物线对称轴平行的直线与该抛物线仅有一个交点,我们把这条直线称为抛物线的切线,已知抛物线经过点![]() ,
,![]() ,且直线
,且直线![]() 是该抛物线的切线,求抛物线的解析式;
是该抛物线的切线,求抛物线的解析式;
(3)已知直线![]() 与(2)中的抛物线交于
与(2)中的抛物线交于![]() ,
,![]() 两点,点
两点,点![]() 的坐标为
的坐标为![]() .求证:
.求证:![]() 为定值.(参考公式:在平面直角坐标系中,已知点
为定值.(参考公式:在平面直角坐标系中,已知点![]() ,
,![]() ,则
,则![]() ,
,![]() 两点之间的距离为
两点之间的距离为![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500m,先到终点
的人原地休息.已知甲先出发2s.在跑步过程中,甲、乙两人的距离y(m)与乙出发的时间t(s)之间的关系
如图所示,给出以下结论:①a=8;②b=92;③c=123.其中正确的是【 】

A.①②③ B.仅有①② C.仅有①③ D.仅有②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.填空:
①![]() 的值为 ;
的值为 ;
②∠AMB的度数为 .
(2)类比探究
如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线于点M.请判断![]() 的值及∠AMB的度数,并说明理由;
的值及∠AMB的度数,并说明理由;
(3)拓展延伸
在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M,若OD=1,OB=![]() ,请直接写出当点C与点M重合时AC的长.
,请直接写出当点C与点M重合时AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形ABCD中,AB=4,∠ABC=60°,∠EAF的两边分别与射线CB、DC相交于点E、F,且∠EAF=60°
(1)如图1,当点E是CB上任意一点时(点E不与B、C重合),求证:BE=CF;
(2)如图2,当点E在CB的延长线上时,且∠EAB=15°,求点F到BC的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一块矩形铁皮,长12dm,宽4dm,在它的四角各切去一个同样的正方形,然后将四周突出部分折起,制作一个无盖方盒,如果要使制作的无盖方盒的侧面积.占矩形铁皮面积的八分之五,设各角切去的正方形的边长为xdm.
(1)用含x的代数式表示,盒底的长为______dm,盒底的宽为______dm;
(2)求x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明为了测量大楼AB的高度,他从点C出发,沿着斜坡面CD走52米到点D处,测得大楼顶部点A的仰角为37°,大楼底部点B的俯角为45°,已知斜坡CD的坡度为i=1:2.4.大楼AB的高度约为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
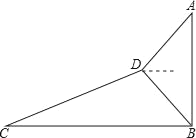
A. 32米B. 35米C. 36米D. 40米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com