解:(1)∵DE是AC的垂直平分线,
∴DA=DC,CE=AE=3cm,…
∴AC=6cm
∵△ABD的周长为13cm
∴AB+BD+AD=13cm,…
即AB+BD+DC=13cm,
∴AB+BC+AC=13+6=19cm,
∴△ABC的周长为19cm…
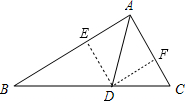
(2)过点D作DE⊥AB,DF⊥AC,垂足分别为E、F…
∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC,
∴DE=DF,…
∴S
△ABD=

•DE•AB=12,
∴DE=DF=3…
∴S
△ABC=

•DF•AC=

×3×6=9…
分析:(1)由在△ABC中,DE是AC的垂直平分线,AE=3cm,根据线段垂直平分线的性质,可得DA=DC,AC=6cm,又由△ABD的周长为13cm,由等量代换即可求得△ABC的周长;
(2)首先过点D作DE⊥AB,DF⊥AC,由AD是它的角平分线,根据角平分线的性质,即可求得DE=DF,由△ABD的面积为12,可求得DE与DF的长,又由AC=6,则可求得△ACD的面积.
点评:此题考查了线段垂直平分线的性质与角平分线的性质.此题难度不大,解题的关键是熟记线段垂直平分线的性质与角平分线的性质定理的应用,注意数形结合思想的应用,注意辅助线的作法.

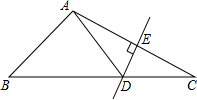
 (2)过点D作DE⊥AB,DF⊥AC,垂足分别为E、F…
(2)过点D作DE⊥AB,DF⊥AC,垂足分别为E、F… •DE•AB=12,
•DE•AB=12, •DF•AC=
•DF•AC= ×3×6=9…
×3×6=9…
