
分析 根据黄金分割点的定义,知AC为较长线段;则AC=$\frac{\sqrt{5}-1}{2}$AB,代入数据即可得出AC的值,然后计算AB-AC即可得到BC.
解答 解:∵C为线段AB的黄金分割点(AC>BC),
∴AC=$\frac{\sqrt{5}-1}{2}$AB=$\frac{\sqrt{5}-1}{2}$×6=3$\sqrt{5}$-3(cm),
∴BC=AB-AC=6-(3$\sqrt{5}$-3)=9-3$\sqrt{5}$(cm).
故答案为(9-3$\sqrt{5}$).
点评 本题考查了黄金分割:把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项(即AB:AC=AC:BC),叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点.其中AC=$\frac{\sqrt{5}-1}{2}$AB≈0.618AB,并且线段AB的黄金分割点有两个.


科目:初中数学 来源: 题型:选择题
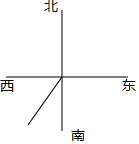 如图,某测绘装置上有一枚指针,原来指向南偏西40°,现把这枚指针按逆时针方向旋转$\frac{1}{4}$圆周,则结果指针指向是( )
如图,某测绘装置上有一枚指针,原来指向南偏西40°,现把这枚指针按逆时针方向旋转$\frac{1}{4}$圆周,则结果指针指向是( )| A. | 南偏东40°方向 | B. | 北偏西50°方向 | C. | 南偏东50°方向 | D. | 东南方向 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
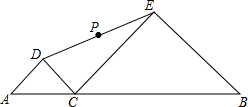 如图,线段AB长为6cm,点C是线段AB上一动点(不与A,B重合),分别以AC和BC为斜边,在AB的同侧作等腰直角三角形△ADC,△CEB,点P是DE的中点,当点C从距离A点1cm处沿AB向右运动至距离B点1cm处时,点P运动的路径长是2cm.
如图,线段AB长为6cm,点C是线段AB上一动点(不与A,B重合),分别以AC和BC为斜边,在AB的同侧作等腰直角三角形△ADC,△CEB,点P是DE的中点,当点C从距离A点1cm处沿AB向右运动至距离B点1cm处时,点P运动的路径长是2cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某班“数学兴趣小组”对函数y=x2-2|x|的图象和性质进行了探究.探究过程如下,请补充完整.
某班“数学兴趣小组”对函数y=x2-2|x|的图象和性质进行了探究.探究过程如下,请补充完整.| x | … | -3 | -$\frac{5}{2}$ | -2 | -1 | 0 | 1 | 2 | $\frac{5}{2}$ | 3 | … |
| y | … | 3 | $\frac{5}{4}$ | m | -1 | 0 | -1 | n | $\frac{5}{4}$ | 3 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
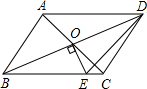 如图,平行四边形ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD交BC于点E.若△CDE的周长为10,则AB+AD的值是( )
如图,平行四边形ABCD的对角线相交于点O,且AB≠AD,过O作OE⊥BD交BC于点E.若△CDE的周长为10,则AB+AD的值是( )| A. | 10 | B. | 15 | C. | 25 | D. | 30 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com