
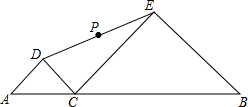
 如图,线段AB长为6cm,点C是线段AB上一动点(不与A,B重合),分别以AC和BC为斜边,在AB的同侧作等腰直角三角形△ADC,△CEB,点P是DE的中点,当点C从距离A点1cm处沿AB向右运动至距离B点1cm处时,点P运动的路径长是2cm.
如图,线段AB长为6cm,点C是线段AB上一动点(不与A,B重合),分别以AC和BC为斜边,在AB的同侧作等腰直角三角形△ADC,△CEB,点P是DE的中点,当点C从距离A点1cm处沿AB向右运动至距离B点1cm处时,点P运动的路径长是2cm. 分析 分别延长AD、BE交于点F,易证四边形CDFE为平行四边形,得出P为CF中点,设点C从距离A点1cm处G沿AB向右运动至距离B点1cm处H,则P的运行轨迹为△FGH的中位线MN.再求出GH的长,运用中位线的性质求出MN的长度即可.
解答 解:如图,分别延长AD、BE交于点F.
∵△ADC和△ECB都是等腰直角三角形,且∠ADC=∠CEB=90°
∵∠A=∠ECB=45°,
∴AF∥CE,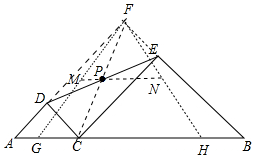
同理,CD∥BF,
∴四边形CDFE为平行四边形,
∴CF与DE互相平分.
∵R为DE的中点,
∴R为CF中点,即在P的运动过程中,R始终为FC的中点,所以R的运行轨迹为三角形FGH的中位线MN.
∵GH=AB-AG-BH=6-1-1=4,
∴MN=$\frac{1}{2}$GH=2,即R的移动路径长为2cm.
故答案为2.
点评 本题考查了等腰直角三角形的性质、三角形中位线的性质、平行四边形的判定和性质,以及动点问题,是中考的热点,解题的关键是正确寻找点R的运动轨迹,属于中考填空题中的压轴题.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在Rt△ABC中,∠ACB=90°,点D在AB边上,将△CBD沿CD折叠,使点B恰好落在AC边上的点E处,若∠A=25°,则∠ADE的度数为( )
如图,在Rt△ABC中,∠ACB=90°,点D在AB边上,将△CBD沿CD折叠,使点B恰好落在AC边上的点E处,若∠A=25°,则∠ADE的度数为( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 10m | B. | 12m | C. | 13m | D. | 15m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2016,1 | B. | 2016,2016 | C. | 1,2016 | D. | 1,1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com