
【题目】某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABCD、线段CD分别表示该产品每千克生产成本y1(单位:元)销售价y2(单位:元)与产量x(单位:kg)之间的函数关系. 
(1)求线段AB所表示的y1与x之间的函数表达式.
(2)当该产品产量为多少时,获得的利润最大?最大利润是多少?
【答案】
(1)解:设线段AB所表示的y1与x之间的函数关系式为y1=k1x+b1,
因为y1=k1x+b1的图象过(0,60)与(90,42),
所以 ![]() ,
,
解方程组得 ![]() ,
,
这个一次函数的表达式为y1=﹣0.2x+60(0≤x≤90);
(2)解:设y2与x之间的函数表达式为y2=k2x+b2,
因为y2=k2x+b2的图象过(0,120)与(130,42),
所以 ![]() ,
,
解方程组得 ![]() ,
,
这个一次函数的表达式为y2=﹣0.6x+120(0≤x≤130),
设产量为xkg时,获得的利润为W元.
①当0≤x≤90时,W=x[(﹣0.6x+120)﹣(﹣0.2x+60)]=﹣0.4(x﹣75)2+2250,
∴当x=75时,W的值最大,最大值为2250;
②当90≤x≤130时,W=x[(﹣0.6x+120)﹣42]=﹣0.6(x﹣65)2+2535,
∴当x=90时,W=﹣0.6(90﹣65)2+2535=2160,
由﹣0.6<0知,当x>65时,W随x的增大而减小,
∴90≤x≤130时,W≤2160,
因此当该产品产量为75kg时,获得的利润最大,最大值为2250.
【解析】(1)根据线段AB经过的两点的坐标利用待定系数法确定一次函数的表达式即可;(2)利用总利润=单位利润×产量,列出有关x的二次函数,求得最值即可.


科目:初中数学 来源: 题型:
【题目】已知A,B两地相距80km,甲,乙两人沿同一条公路从A地出发到B地,乙骑自行车,甲骑摩托车.图中DE,OC分别表示甲,乙离开A地的路程s(km)与时间t(h)的函数关系,根据图象得出的下列信息错误的是( )
A.乙到达B地时甲距A地120km.
B.乙出发1.8小时被甲追上.
C.甲,乙相距20km时,t为2.4h.
D.甲的速度是乙的速度的 ![]() 倍.
倍.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年是第39个植树节,我们提出了“追求绿色时尚,走向绿色文明”的倡议.某校为积极响应这一倡议,立即在八、九年级开展征文活动,校团委对这两个年级各班内的投稿情况进行统计,并制成了如图所示的两幅不完整的统计图. 
(1)求扇形统计图中投稿3篇的班级个数所对应的扇形的圆心角的度数.
(2)求该校八、九年级各班在这一周内投稿的平均篇数,并将该条形统计图补充完整.
(3)在投稿篇数最多的4个班中,八、九年级各有两个班,校团委准备从这四个班中选出两个班参加全校的表彰会,请你用列表法或画树状图的方法求出所选两个班正好不在同一年级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O是正方形ABCD两对角线的交点,分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG、OE为邻边作正方形OEFG,连接AG,DE.
(1)求证:DE⊥AG;
(2)正方形ABCD固定,将正方形OEFG绕点O逆时针旋转α角(0°<α<360°)得到正方形OE′F′G′,如图2.
①在旋转过程中,当∠OAG′是直角时,求α的度数;
②若正方形ABCD的边长为1,在旋转过程中,求AF′长的最大值和此时α的度数,直接写出结果不必说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB=4,∠BAC=30°,AC交⊙O于D,D是AC的中点. 
(1)过点D作DE⊥BC,垂足为E,求证:直线DE是⊙O的切线;
(2)求 ![]() 与线段DE、BE围成的阴影面积.
与线段DE、BE围成的阴影面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直角△ABC的三个顶点分别是:A(﹣3,1),B(0,3),C(0,1) 
(1)将△ABC以点O为旋转中心顺时针旋转90°,画出旋转后对应的△A1B1C1;
(2)分别连结AB1 , BA1后,求四边形ABA1B1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,梯形ABCD中,AB∥DC,∠B=90°,AD=15,AB=16,BC=12,点E是边AB上的动点,点F是射线CD上一点,射线ED和射线AF交于点G,且∠AGE=∠DAB.
(1)求线段CD的长;
(2)如果△AEC是以EG为腰的等腰三角形,求线段AE的长;
(3)如果点F在边CD上(不与点C、D重合),设AE=x,DF=y,求y关于x的函数解析式,并写出x的取值范围.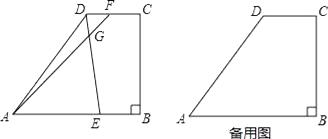
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的图象向左平移5个单位或向右平移1个单位后都会经过原点,则此抛物线的对称轴与x轴的交点的横坐标是( )
A.2
B.﹣2
C.3
D.﹣3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com