
 如图,某农户准备建一个长方形养鸡场,养鸡场的一边靠墙,墙对面有一个2m宽的门,另三边用竹篱笆围成,篱笆总长33m.围成长方形的养鸡场除门之外四周不能有空隙.
如图,某农户准备建一个长方形养鸡场,养鸡场的一边靠墙,墙对面有一个2m宽的门,另三边用竹篱笆围成,篱笆总长33m.围成长方形的养鸡场除门之外四周不能有空隙.分析 (1)先设养鸡场的宽为xm,得出长方形的长,再根据面积公式列出方程,求出x的值即可,注意x要符合题意;
(2)先设养鸡场的宽为xm,得出长方形的长,再根据面积公式列出方程,判断出△的值,即可得出答案;
(3)根据实际问题当0<a<15时,当15≤a<20时,当a≥20时,三种情况进行讨论,得出符合条件的值即可.
解答 解:(1)设养鸡场的宽为xm,根据题意得:
x(33-2x+2)=150,
解得:x1=10,x2=7.5,
当x1=10时,33-2x+2=15<18,
当x2=7.5时33-2x+2=20>18,(舍去),
则养鸡场的宽是10m,长为15m.
(2)设养鸡场的宽为xm,根据题意得:
x(33-2x+2)=200,
整理得:2x2-35x+200=0,
△=(-35)2-4×2×200=1225-1600=-375<0,
因为方程没有实数根,
所以围成养鸡场的面积不能达到200m2;
(3)当0<a<15时,不能围成一个长方形养鸡场;
当15≤a<20时,可以围成一个长方形养鸡场;
当a≥20时,可以围成2个长方形养鸡场.
点评 此题考查了一元二次方程的应用,读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程是解题的关键,注意宽的取值范围.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
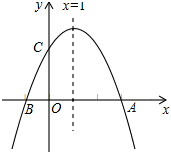 如图:二次函数y=ax2+bx+c的图象与x轴交A、B两点,与y轴交于C点,且对称轴为x=1,点B的坐标是(-1,0),则下面四个结论:①2a+b=0,②4a-2b+c<0,③ac<0,④当y<0时,x<-1或x>3,其中正确的个数是( )
如图:二次函数y=ax2+bx+c的图象与x轴交A、B两点,与y轴交于C点,且对称轴为x=1,点B的坐标是(-1,0),则下面四个结论:①2a+b=0,②4a-2b+c<0,③ac<0,④当y<0时,x<-1或x>3,其中正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图一个矩形减去一个以宽为边长的正方形后,所剩下的矩形与原矩形相似,则原矩形的长与宽的比值为( )
如图一个矩形减去一个以宽为边长的正方形后,所剩下的矩形与原矩形相似,则原矩形的长与宽的比值为( )| A. | $\frac{{3+\sqrt{5}}}{2}$ | B. | $\frac{{\sqrt{5}-1}}{2}$ | C. | $\frac{{3-\sqrt{5}}}{2}$ | D. | $\frac{{\sqrt{5}+1}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=25,b=-25 | B. | a=0,b=-25 | C. | a=25,b=25 | D. | a=0,b=25 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
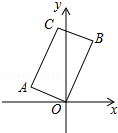 如图,在矩形AOBC中,点A的坐标是(-2,1),点C的纵坐标是4,则B、C两点的坐标分别是( )
如图,在矩形AOBC中,点A的坐标是(-2,1),点C的纵坐标是4,则B、C两点的坐标分别是( )| A. | ($\frac{3}{2}$,3)、(-$\frac{2}{3}$,4) | B. | ($\frac{7}{4},\frac{7}{2}$)、(-$\frac{1}{2},4$) | C. | ($\frac{7}{4},\frac{7}{2}$)、(-$\frac{2}{3},4$) | D. | ($\frac{3}{2},3$)、(-$\frac{1}{2},4$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com