
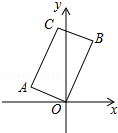
 如图,在矩形AOBC中,点A的坐标是(-2,1),点C的纵坐标是4,则B、C两点的坐标分别是( )
如图,在矩形AOBC中,点A的坐标是(-2,1),点C的纵坐标是4,则B、C两点的坐标分别是( )| A. | ($\frac{3}{2}$,3)、(-$\frac{2}{3}$,4) | B. | ($\frac{7}{4},\frac{7}{2}$)、(-$\frac{1}{2},4$) | C. | ($\frac{7}{4},\frac{7}{2}$)、(-$\frac{2}{3},4$) | D. | ($\frac{3}{2},3$)、(-$\frac{1}{2},4$) |
分析 首先过点A作AD⊥x轴于点D,过点B作BE⊥x轴于点E,过点C作CF∥y轴,过点A作AF∥x轴,交点为F,易得△CAF≌△BOE,△AOD∽△OBE,然后由相似三角形的对应边成比例,求得答案.
解答 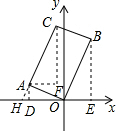 解:过点A作AD⊥x轴于点D,过点B作BE⊥x轴于点E,过点C作CF∥y轴,过点A作AF∥x轴,交点为F,延长CA交x轴于点H,
解:过点A作AD⊥x轴于点D,过点B作BE⊥x轴于点E,过点C作CF∥y轴,过点A作AF∥x轴,交点为F,延长CA交x轴于点H,
∵四边形AOBC是矩形,
∴AC∥OB,AC=OB,
∴∠CAF=∠BOE=∠CHO,
在△ACF和△OBE中,
$\left\{\begin{array}{l}{∠F=∠BEO=90°}\\{∠CAF=∠BOE}\\{AC=OB}\end{array}\right.$,
∴△CAF≌△BOE(AAS),
∴BE=CF=4-1=3,
∵∠AOD+∠BOE=∠BOE+∠OBE=90°,
∴∠AOD=∠OBE,
∵∠ADO=∠OEB=90°,
∴△AOD∽△OBE,
∴$\frac{AD}{OE}$=$\frac{OD}{BE}$,
即$\frac{1}{OE}$=$\frac{2}{3}$,
∴OE=$\frac{3}{2}$,
即点B($\frac{3}{2}$,3),
∴AF=OE=$\frac{3}{2}$,
∴点C的横坐标为:-(2-$\frac{3}{2}$)=-$\frac{1}{2}$,
∴点C(-$\frac{1}{2}$,4).
故选D.
点评 此题考查了矩形的性质、全等三角形的判定与性质以及相似三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.


科目:初中数学 来源: 题型:解答题
 如图,某农户准备建一个长方形养鸡场,养鸡场的一边靠墙,墙对面有一个2m宽的门,另三边用竹篱笆围成,篱笆总长33m.围成长方形的养鸡场除门之外四周不能有空隙.
如图,某农户准备建一个长方形养鸡场,养鸡场的一边靠墙,墙对面有一个2m宽的门,另三边用竹篱笆围成,篱笆总长33m.围成长方形的养鸡场除门之外四周不能有空隙.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 三条中线的交点 | B. | 三条高的交点 | ||
| C. | 三条内角平分线的交点 | D. | 三边中垂线的交点 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
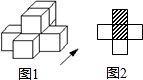 如果用□表示一个立方体,用阴影■表示三个立方体叠加,那么如图1所示由7个立方体叠成的几何体,小明同学从上方观察,画出的平面图形如图2所示.请画出从正前方和左面观察到的平面图形.
如果用□表示一个立方体,用阴影■表示三个立方体叠加,那么如图1所示由7个立方体叠成的几何体,小明同学从上方观察,画出的平面图形如图2所示.请画出从正前方和左面观察到的平面图形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
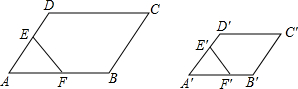 如图,?ABCD∽?A′B′C′D′,E、F分别是DA、AB的中点,E′、F′分别是D′A′、A′B′的中点,求证:五边形BCDEF∽五边形B′C′D′E′F′.
如图,?ABCD∽?A′B′C′D′,E、F分别是DA、AB的中点,E′、F′分别是D′A′、A′B′的中点,求证:五边形BCDEF∽五边形B′C′D′E′F′.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com