
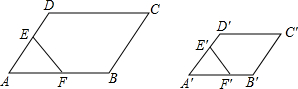
 如图,?ABCD∽?A′B′C′D′,E、F分别是DA、AB的中点,E′、F′分别是D′A′、A′B′的中点,求证:五边形BCDEF∽五边形B′C′D′E′F′.
如图,?ABCD∽?A′B′C′D′,E、F分别是DA、AB的中点,E′、F′分别是D′A′、A′B′的中点,求证:五边形BCDEF∽五边形B′C′D′E′F′. 分析 根据相似多边形的性质得到∠A=∠A′,$\frac{AD}{A′D′}$=$\frac{AB}{A′B′}$,根据中点的性质得到△AEF∽△A′E′F′,根据相似多边形的判定定理证明结论.
解答 证明:∵?ABCD∽?A′B′C′D′,
∴∠A=∠A′,$\frac{AD}{A′D′}$=$\frac{AB}{A′B′}$,又E、F分别是DA、AB的中点,E′、F′分别是D′A′、A′B′的中点,
∴$\frac{AE}{A′E′}$=$\frac{AF}{A′F′}$,又∠A=∠A′,
∴△AEF∽△A′E′F′,
∴$\frac{EF}{E′F′}$=$\frac{DE}{D′E′}$=$\frac{AD}{A′D′}$,∠AEF=∠A′E′F′,∠AFE=∠A′F′E′,
∴∠DEF=∠D′E′F′,∠BFE=∠B′F′E′,
∴五边形BCDEF∽五边形B′C′D′E′F′.
点评 本题考查的是相似多边形的判定和性质,掌握对应角相等、对应边成比例的两个多边形相似是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | a=25,b=-25 | B. | a=0,b=-25 | C. | a=25,b=25 | D. | a=0,b=25 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
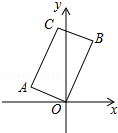 如图,在矩形AOBC中,点A的坐标是(-2,1),点C的纵坐标是4,则B、C两点的坐标分别是( )
如图,在矩形AOBC中,点A的坐标是(-2,1),点C的纵坐标是4,则B、C两点的坐标分别是( )| A. | ($\frac{3}{2}$,3)、(-$\frac{2}{3}$,4) | B. | ($\frac{7}{4},\frac{7}{2}$)、(-$\frac{1}{2},4$) | C. | ($\frac{7}{4},\frac{7}{2}$)、(-$\frac{2}{3},4$) | D. | ($\frac{3}{2},3$)、(-$\frac{1}{2},4$) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{2}{3}$>-$\frac{3}{4}$ | B. | -$\frac{1}{3}$<-0.3 | C. | -(-2)>+(-3) | D. | -(-2.5)<|-2$\frac{1}{4}$| |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
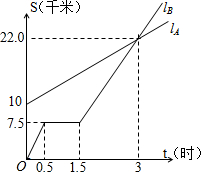 如图,lA lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
如图,lA lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
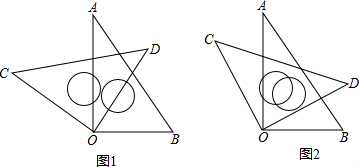
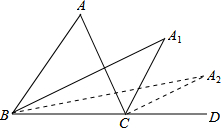 如图,△A1BC一个内角的平分线和一个外角的平分线相交得到点A2,△A2BC的内外角平分线相交,得到点A3,…,用∠A表示∠A2015.
如图,△A1BC一个内角的平分线和一个外角的平分线相交得到点A2,△A2BC的内外角平分线相交,得到点A3,…,用∠A表示∠A2015.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com