
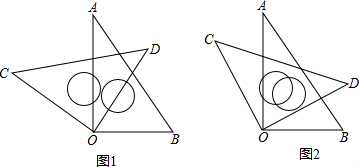
分析 (1)由∠AOB=∠COD都减去∠AOD,即可得出答案;
(2)根据平行线的性质得出即可;
(3)根据三角形内角和定理求出∠AQN,求出∠AQO,根据三角形内角和定理求出即可.
解答 (1)解:如图1,∠AOC=∠BOD,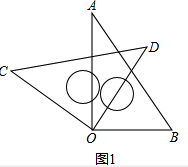
理由是:∵∠DOC=∠AOB=90°,
∴∠DOC-∠AOD=∠AOB-∠AOD,
∴∠AOC=∠BOD;
(2)如图2,DO⊥AB,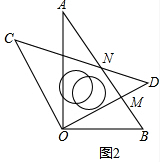
证明:
∵CO∥AB,∠COD=90°,
∴∠NMD=∠COD=90°,
∴DO⊥AB;
(3)如图3,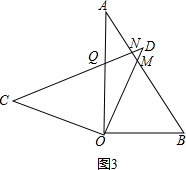
解:能使CD⊥AB,
理由是:∵CD⊥AB,
∴∠ANQ=90°,
∵∠A=30°,
∴∠AQN=180°-90°-30°=60°,
∴∠CQO=∠AQN=60°,
∵∠C=45°,
∴∠AOC=180°-∠CQO-∠C=180°-60°-45°=75°.
点评 本题考查了三角形内角和定理,平行线的性质,垂直定义的应用,能根据三角形内角和定理求出各个角的度数是解此题的关键.


科目:初中数学 来源: 题型:选择题
| A. | a2+a=a3 | B. | (a3)2=a5 | C. | $\sqrt{3}$×$\sqrt{3}$=3 | D. | $\sqrt{16}$-$\sqrt{9}$=$\sqrt{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 三条中线的交点 | B. | 三条高的交点 | ||
| C. | 三条内角平分线的交点 | D. | 三边中垂线的交点 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
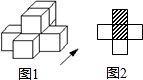 如果用□表示一个立方体,用阴影■表示三个立方体叠加,那么如图1所示由7个立方体叠成的几何体,小明同学从上方观察,画出的平面图形如图2所示.请画出从正前方和左面观察到的平面图形.
如果用□表示一个立方体,用阴影■表示三个立方体叠加,那么如图1所示由7个立方体叠成的几何体,小明同学从上方观察,画出的平面图形如图2所示.请画出从正前方和左面观察到的平面图形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
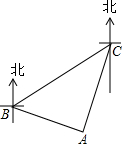 如图,某轮船航行至点A时,测得:轮船在小岛B的南偏东75°的方向,在航海塔C的南偏西20°,又知航海塔C在小岛B的北偏东65°的方向,下列结论正确的是( )
如图,某轮船航行至点A时,测得:轮船在小岛B的南偏东75°的方向,在航海塔C的南偏西20°,又知航海塔C在小岛B的北偏东65°的方向,下列结论正确的是( )| A. | ∠ABC=50° | B. | ∠BCA=55° | C. | ∠BAC=95° | D. | 以上都正确 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
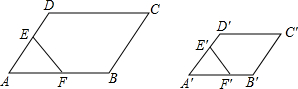 如图,?ABCD∽?A′B′C′D′,E、F分别是DA、AB的中点,E′、F′分别是D′A′、A′B′的中点,求证:五边形BCDEF∽五边形B′C′D′E′F′.
如图,?ABCD∽?A′B′C′D′,E、F分别是DA、AB的中点,E′、F′分别是D′A′、A′B′的中点,求证:五边形BCDEF∽五边形B′C′D′E′F′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com