
| A. | 三条中线的交点 | B. | 三条高的交点 | ||
| C. | 三条内角平分线的交点 | D. | 三边中垂线的交点 |
分析 画出任意一个三角形,过三角形的内心任意画一条直线,分△ABC的周长为m、n两部分,然后三角形的面积公式求得两部分的面积即可.
解答 解:如图所示:△ABC为任意三角形,⊙O为三角形的内切圆,过点O任意画一条直线.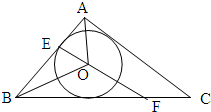 设:BE+BF=m,AE+AC+FC=n,设⊙O的半径为R.
设:BE+BF=m,AE+AC+FC=n,设⊙O的半径为R.
∴△BEF的面积=$\frac{1}{2}(BE+BF)•R$=$\frac{1}{2}mR$,△ABC的面积=$\frac{1}{2}(AB+BC+AC)R$=$\frac{1}{2}(m+n)R$.
∴四边形AEFC的面积=△ABC的面积-△BEF的面积=$\frac{1}{2}nR$.
∴△BEF的面积:四边形AEFC的面积=$\frac{1}{2}mR$=m:n.
∴过三角形内心的直线将三角形的面积和周长同时分为$\frac{m}{n}$的两部分.
故选:C.
点评 本题主要考查的是角平分线的性质的应用,利用角平分线的性质求得三角形BEF和四边形AEFC的面积是解题的关键.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
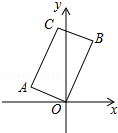 如图,在矩形AOBC中,点A的坐标是(-2,1),点C的纵坐标是4,则B、C两点的坐标分别是( )
如图,在矩形AOBC中,点A的坐标是(-2,1),点C的纵坐标是4,则B、C两点的坐标分别是( )| A. | ($\frac{3}{2}$,3)、(-$\frac{2}{3}$,4) | B. | ($\frac{7}{4},\frac{7}{2}$)、(-$\frac{1}{2},4$) | C. | ($\frac{7}{4},\frac{7}{2}$)、(-$\frac{2}{3},4$) | D. | ($\frac{3}{2},3$)、(-$\frac{1}{2},4$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com