
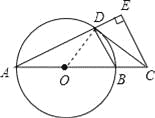
【题目】如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.
(1)求证:∠BDC=∠A;
(2)若CE=4,DE=2,求AD的长.

【答案】(1)证明过程见解析;(2)6.
【解析】试题分析:(1)连接OD,由CD是⊙O切线,得到∠ODC=90°,根据AB为⊙O的直径,得到∠ADB=90°,等量代换得到∠BDC=∠ADO,根据等腰直角三角形的性质得到∠ADO=∠A,即可得到结论;(2)根据垂直的定义得到∠E=∠ADB=90°,根据平行线的性质得到∠DCE=∠BDC,根据相似三角形的性质得到![]() ,解方程即可得到结论.
,解方程即可得到结论.
试题解析:(1)连接OD, ∵CD是⊙O切线, ∴∠ODC=90°, 即∠ODB+∠BDC=90°,
∵AB为⊙O的直径, ∴∠ADB=90°, 即∠ODB+∠ADO=90°, ∴∠BDC=∠ADO,
∵OA=OD, ∴∠ADO=∠A, ∴∠BDC=∠A;
(2)∵CE⊥AE, ∴∠E=∠ADB=90°, ∴DB∥EC, ∴∠DCE=∠BDC, ∵∠BDC=∠A, ∴∠A=∠DCE,
∵∠E=∠E, ∴△AEC∽△CED, ∴![]() , ∴EC2=DEAE, ∴16=2(2+AD), ∴AD=6.
, ∴EC2=DEAE, ∴16=2(2+AD), ∴AD=6.


科目:初中数学 来源: 题型:
【题目】计算(x-5y)(3x+4y)的结果正确的是( )
A. 3x2-20y2 B. 3x2-15xy+20y2
C. 3x2-11xy-20y2 D. 3x2+20y2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据国家统计局数据,2018年全年国内生产总值为90.3万亿,比2017年增长6.6%.假设国内生产总值的年增长率保持不变,则国内生产总值首次突破100万亿的年份是( )
A. 2019年B. 2020年C. 2021年D. 2022年
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,抛物线![]() (
(![]() )交x轴于A、B两点,交y轴于点C,且对称轴为直线x=―2 .
)交x轴于A、B两点,交y轴于点C,且对称轴为直线x=―2 .
(1)求该抛物线的解析式及顶点D的坐标;
(2)若点P(0,t)是y轴上的一个动点,请进行如下探究:
探究一:如图1,设△PAD的面积为S,令W=t·S,当0<t<4时,W是否有最大值?如果有,求出W的最大值和此时t的值;如果没有,说明理由;
探究二:如图2,是否存在以P、A、D为顶点的三角形与Rt△AOC相似?如果存在,求点P的坐标;如果不存在,请说明理由.
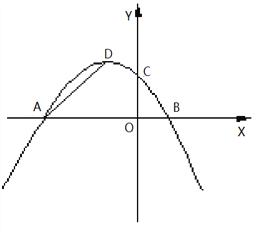

图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大型超市从生产基地以每千克a元的价格购进一种水果m千克,运输过程中重量损失了10%,超市在进价的基础上増加了30%作为售价,假定不计超市其他费用,那么售完这种水果,超市获得的利润是_____元(用含m、a的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com