
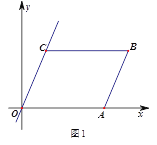
【题目】如图,在平面直角坐标系中,四边形OABC是平行四边形.直线L经过O、C两点.点A的坐标为(8,0),点B的坐标为(11,4),动点P在线段OA上从点O出发以每秒1个单位的速度向点A运动,同时动点Q从点A出发以每秒2个单位的速度沿A→B→C的方向向点C运动,过点P作PM垂直于x轴,与折线O一C﹣B相交于点M.当Q、M两点相遇时,P、Q两点停止运动,设点P、Q运动的时间为t秒(t>0).△MPQ的面积为S.
(1)点C的坐标为 ,直线L的解析式为 .
(2)试求点Q与点M相遇前S与t的函数关系式,并写出相应的t的取值范围.
(3)试求题(2)中当t为何值时,S的值最大,并求出S的最大值.
(4)随着P、Q两点的运动,当点M在线段CB上运动时,设PM的延长线与直线L相交于点N.试探究:当t为何值时,△QMN为等腰三角形?请直接写出t的值.



【答案】(1)(3,4),y= ![]() x;(2)①当0<t≤
x;(2)①当0<t≤![]() ,S=
,S= ![]() t2+
t2+ ![]() t;②当
t;②当![]() <t≤3时,S= -2t2+
<t≤3时,S= -2t2+![]() t, ③当点Q与点M相遇时,S=﹣6t+32;(3) 当
t, ③当点Q与点M相遇时,S=﹣6t+32;(3) 当![]() 时,S有最大值,最大值为
时,S有最大值,最大值为![]() .(4) 当t=
.(4) 当t=![]() 时,△QMN为等腰三角形.
时,△QMN为等腰三角形.
【解析】(1)由平行四边形的性质和点A、B的坐标便可求出C点坐标,将C点坐标代入正比例函数即可求得直线l的解析式;
(2)根据题意,得OP=t,AQ=2t,根据t的取值范围不同分三种情况分别进行讨论,得到三种S关于t的函数,解题时注意t的取值范围;
(3)分别根据三种函数解析式求出当t为何值时,S最大,然后比较三个最大值,可知当t=![]() 时,S有最大值,最大值为
时,S有最大值,最大值为![]() ;
;
(4)根据题意并细心观察图象,分两种情况讨论可知:当t=![]() 时,△QMN为等腰三角形.
时,△QMN为等腰三角形.
解:(1)由题意知:点A的坐标为(8,0),点B的坐标为(11.4),
且OA=BC,故C点坐标为C(3,4),设直线l的解析式为y=kx,将C点坐标代入y=kx,解得k=![]() ,
,
∴直线l的解析式为y= ![]() x;故答案为:(3,4),y=
x;故答案为:(3,4),y= ![]() x;
x;

(2)根据题意,得OP=t,AQ=2t.分四种情况讨论:
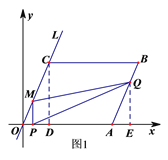
①当0<t≤![]() 时,如图1,M点的坐标是(t,
时,如图1,M点的坐标是(t,![]() t).过点C作CD⊥x轴于D,过点Q作QE⊥x轴于E,可得△AEQ∽△ODC,∴
t).过点C作CD⊥x轴于D,过点Q作QE⊥x轴于E,可得△AEQ∽△ODC,∴ ![]() =
= ![]() =
=![]() ,∴
,∴ ![]() =
= ![]() =
=![]() ,∴AE =
,∴AE =![]() ,EQ=
,EQ= ![]() t,∴Q点的坐标是(8+
t,∴Q点的坐标是(8+ ![]() t,
t,![]() t),∴PE=8+
t),∴PE=8+![]() t-t= 8+
t-t= 8+![]() t,∴S=
t,∴S=![]() ·MP·PE=
·MP·PE=![]() ·
·![]() t·(8+
t·(8+![]() t)=
t)= ![]() t2+
t2+ ![]() t;
t;
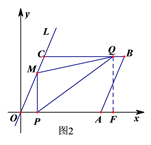
②当![]() <t≤3时,如图2,过点Q作QF⊥x轴于F,∵BQ=2t﹣5,∴OF=11﹣(2t﹣5)=16﹣2t,
<t≤3时,如图2,过点Q作QF⊥x轴于F,∵BQ=2t﹣5,∴OF=11﹣(2t﹣5)=16﹣2t,
∴Q点的坐标是(16﹣2t,4),∴PF=16﹣2t﹣t=16﹣3t,
∴S=![]() ·MP·PF=
·MP·PF=![]() ·
·![]() t·(16-3t)= -2t2+
t·(16-3t)= -2t2+![]() t,
t,
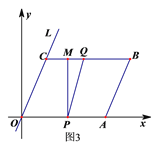
③当点Q与点M相遇时,16﹣2t=t,解得t =![]() .当3<t<
.当3<t<![]() 时,如图3,MQ=16﹣2t﹣t=16﹣3t,MP=4.S=
时,如图3,MQ=16﹣2t﹣t=16﹣3t,MP=4.S=![]() ·MP·PF =
·MP·PF =![]() ·4·(16-3t)=﹣6t+32;
·4·(16-3t)=﹣6t+32;
(3)解:① 当![]() 时,
时,![]() ,∵
,∵![]() ,抛物线开口向上,对称轴为直线
,抛物线开口向上,对称轴为直线![]() , ∴ 当
, ∴ 当![]() 时,S随t的增大而增大.
时,S随t的增大而增大.
∴ 当![]() 时,S有最大值,最大值为
时,S有最大值,最大值为![]() .
.
②当![]() 时,
时,![]() 。∵
。∵![]() ,抛物线开口向下.
,抛物线开口向下.
∴当![]() 时,S有最大值,最大值为
时,S有最大值,最大值为![]() .
.
③当![]() 时,
时,![]() ,∵
,∵![]() .∴S随t的增大而减小.
.∴S随t的增大而减小.
又∵当![]() 时,S=14.当
时,S=14.当![]() 时,S=0.∴
时,S=0.∴![]() .
.
综上所述,当![]() 时,S有最大值,最大值为
时,S有最大值,最大值为![]() .
.
(4)M、Q在BC边上运动且没有相遇时,如图4,CM=t-3,BQ= 2t-5,MN=![]() (t-3),∴MQ= 8-(t-3)-(2t-5)= 16-3t,∴只有
(t-3),∴MQ= 8-(t-3)-(2t-5)= 16-3t,∴只有![]() (t-3)=16-3t,即当t=
(t-3)=16-3t,即当t=![]() 时,△QMN为等腰三角形.
时,△QMN为等腰三角形.
“点睛”本题是二次函数的综合题,其中涉及到的知识点有抛物线最大值的求法和动点问题等知识点,是各地中考的热点和难点,解题时注意数形结合和分类讨论等数学思想的运用,同学们要加强训练,属于难题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图①,在△ABC 中,AD平分∠BAC,AE⊥BC,∠B=40°,∠C=70°.
(1)求∠DAE的度数;
(2)如图②,若把“AE⊥BC”变成“点F在DA的延长线上,FE⊥BC”,其它条件不变,求∠DFE的度数. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC外侧作直线AP,点B关于直线AP的对称点为D,连接BD,CD,其中CD交直线AP于点E. 
(1)依题意补全图1;
(2)若∠PAB=30°,求∠ACE的度数;
(3)如图2,若60°<∠PAB<120°,判断由线段AB,CE,ED可以构成一个含有多少度角的三角形,并证明. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,AB=6,第一次平移长方形ABCD沿AB的方向向右平移5个单位,得到长方形A1B1C1D1 , 第2次平移将长方形A1B1C1D1沿A1B1的方向向右平移5个单位,得到长方形A2B2C2D2…,第n次平移将长方形An﹣1Bn﹣1Cn﹣1Dn﹣1沿An﹣1Bn﹣1的方向平移5个单位,得到长方形AnBnCnDn(n>2),若ABn的长度为56,则n= 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)某班“数学兴趣小组”对函数![]() 的图像和性质进行了探究,探究过程如下,请补充完整.
的图像和性质进行了探究,探究过程如下,请补充完整.
(1)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
| … |
|
|
|
| 0 | 1 | 2 | 3 | 4 | … |
| … | 3 |
|
|
| 0 |
| 0 |
| 3 | … |
其中,![]() =____________.
=____________.
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图像的一部分,请画出该图像的另一部分.
(3)观察函数图像,写出两条函数的性质:

(4)进一步探究函数图像发现:
①函数图像与![]() 轴有__________个交点,所以对应方程
轴有__________个交点,所以对应方程![]() 有___________个实数根;
有___________个实数根;
②方程![]() 有___________个实数根;
有___________个实数根;
③关于![]() 的方程
的方程![]() 有4个实数根,
有4个实数根,![]() 的取值范围是_______________________
的取值范围是_______________________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC、BD相交于点O,增加下列条件后,ABCD不一定是菱形的是( ) 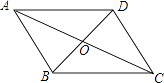
A.DC=BC
B.AC⊥BD
C.AB=BD
D.∠ADB=∠CDB
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com