
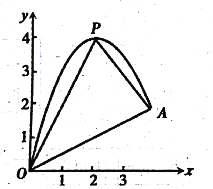
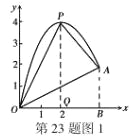
【题目】如图,一小球从斜坡D点处抛出,球的抛出路线可以用二次函数)y=-x2+4x刻画,斜坡OA可以用一次函数y=![]() 刻画.
刻画.
(1)请用配方法求二次函数图象的最高点P的坐标;
(2)小球的落点是A,求点A的坐标
(3)连接抛物线的最高点P与点O、A得△POA,求△POA的面积;
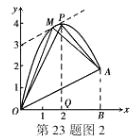
(4)在OA上方的抛物线上存在一点M(M与P不重合),△MOA的面积等于△POA的面积,请直接写出点M的坐标。
【答案】(1)、P(2,4);(2)、A(![]() ,
,![]() );(3)、
);(3)、![]() ;(4)、M(
;(4)、M(![]() ,
,![]() ).
).
【解析】
试题分析:(1)、利用配方法将二次函数配成顶点式,从而得出点P的坐标;(2)、将二次函数和一次函数联立成方程组,从而求出点的坐标;(3)、作PQ⊥x轴于点Q,AB⊥x轴于点B,根据△AOP的面积=△POQ的面积+梯形PQBA的面积-△AOB的面积得出答案;(4)、过P作OA的平行线,交抛物线于点M,连接OM、AM,得出△MOA的面积等于△POA的面积,设直线PM的解析式为y=![]() x+b,将点P坐标代入得出解析式,然后与二次函数联立成方程组得出答案.
x+b,将点P坐标代入得出解析式,然后与二次函数联立成方程组得出答案.
试题解析:(1)、由题意得:y=-![]() +4x=-
+4x=-![]() +4 ∴点P的坐标为(2,4)
+4 ∴点P的坐标为(2,4)
(2)、联立两解析式可得: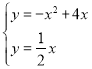 解得:
解得:![]() 或
或![]()
∴点A的坐标为(![]() ,
,![]() )
)
(3)、如图1,作PQ⊥x轴于点Q,AB⊥x轴于点B
![]() =
=![]() ×2×4+
×2×4+![]() ×(
×(![]() +4)×(
+4)×(![]() -2)-
-2)-![]() ×
×![]() ×
×![]() =4+
=4+![]() -
-![]() =
=![]() .
.
(4)、如图2,过P作OA的平行线,交抛物线于点M,连接OM、AM,则△MOA的面积等于△POA的面积
设直线PM的解析式为:y=![]() x+b ∵点P的坐标为(2,4) ∴b=3
x+b ∵点P的坐标为(2,4) ∴b=3
∴直线PM的解析式为:y=![]() x+3
x+3
由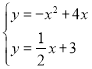 解得:
解得:![]() 或
或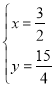 ∴点M的坐标为:(
∴点M的坐标为:(![]() ,
,![]() )
)


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,小明所在学校的旗杆BD高约为13米,距离旗杆20米处刚好有一棵高约为3米的香樟树AE.活动课上,小明有意在旗杆与香樟树之间的连线上来回踱步,发现有一个位置到旗杆顶部与树顶的距离相等.请你求出该位置与旗杆之间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一艘轮船自西向东航行,在A处测得小岛P的方位是北偏东75°,航行7海里后,在B处测得小岛P的方位是北偏东60°,若小岛周围3.8海里内有暗礁,问该船一直向东航行,有无触礁的危险?并说明原因.
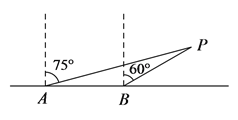

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D,F在线段AB上,点E,G分别在线段BC和AC上,CD∥EF,∠1=∠2. 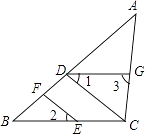
(1)判断DG与BC的位置关系,并说明理由;
(2)若DG是∠ADC的平分线,∠3=85°,且∠DCE:∠DCG=9:10,试说明AB与CD有怎样的位置关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有3cm,3cm,6cm,6cm,12cm,12cm的六条线段,任选其中的三条线段组成一个等腰三角形,则最多能组成等腰三角形的个数为( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
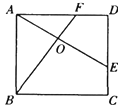
【题目】如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列四个结论:①AE=BF;②AE⊥BF;③ AO=OE;④ ![]() 。
。
其中正确的有______________(只填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一元二次方程ax2+bx+c=0(a≠0)能用公式法求解,那么必须满足的条件是( )
A.b2-4ac≥0
B.b2-4ac≤0
C.b2-4ac>0
D.b2-4ac<0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com