
【题目】如图,点D,F在线段AB上,点E,G分别在线段BC和AC上,CD∥EF,∠1=∠2. 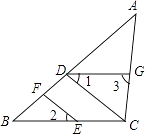
(1)判断DG与BC的位置关系,并说明理由;
(2)若DG是∠ADC的平分线,∠3=85°,且∠DCE:∠DCG=9:10,试说明AB与CD有怎样的位置关系?
【答案】
(1)解:DG∥BC.
理由:∵CD∥EF,
∴∠2=∠BCD.
∵∠1=∠2,
∴∠1=∠BCD,
∴DG∥BC
(2)解:CD⊥AB.
理由:∵由(1)知DG∥BC,∠3=85°,
∴∠BCG=180°﹣85°=95°.
∵∠DCE:∠DCG=9:10,
∴∠DCE=95°× ![]() =45°.
=45°.
∵DG是∠ADC的平分线,
∴∠ADC=2∠CDG=90°,
∴CD⊥AB
【解析】(1)先根据CD∥EF得出∠2=∠BCD,再由∠1=∠2得出∠1=∠BCD,进而可得出结论;(2)根据DG∥BC,∠3=85°得出∠BCG的度数,再由∠DCE:∠DCG=9:10得出∠DCE的度数,由DG是∠ADC的平分线可得出∠ADC的度数,由此得出结论.
【考点精析】解答此题的关键在于理解平行线的判定与性质的相关知识,掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】2017年“一带一路”建设取得重大进展,据商务部数据显示,今年前11个月,我国与沿线国家贸易额达9831亿美元,这一数据用科学记数法可表示为_____美元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线交AB于M,交AC于N.
(1)若∠ABC=70°,则∠MNA的度数是__.
(2)连接NB,若AB=8cm,△NBC的周长是14cm.
①求BC的长;
②在直线MN上是否存在P,使由P、B、C构成的△PBC的周长值最小?若存在,标出点P的位置并求△PBC的周长最小值;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“支付宝”与“滴滴打车”联合推出优惠,“滴滴打车”一时红遍大江南北.据统计,2016年“滴滴打车”账户流水总金额达到4730000000元,用科学记数法表示为______元.
查看答案和解析>>
科目:初中数学 来源: 题型:
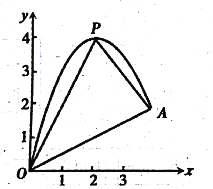
【题目】如图,一小球从斜坡D点处抛出,球的抛出路线可以用二次函数)y=-x2+4x刻画,斜坡OA可以用一次函数y=![]() 刻画.
刻画.
(1)请用配方法求二次函数图象的最高点P的坐标;
(2)小球的落点是A,求点A的坐标
(3)连接抛物线的最高点P与点O、A得△POA,求△POA的面积;
(4)在OA上方的抛物线上存在一点M(M与P不重合),△MOA的面积等于△POA的面积,请直接写出点M的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A. 直线外一点与直线上各点连接的线段中,垂线最短 B. 点到直线的距离是这点到直线的垂线段
C. 过一点有且只有一条直线与已知直线平行 D. 在同一平面内,垂直于同一条直线的两直线平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若A,B,C是直线l上的三点,P是直线l外一点,且PA=6cm,PB=5cm,PC=4cm,则点P到直线l的距离( )
A.等于4cm
B.大于4cm而小于5cm
C.不大于4cm
D.小于4cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com