
分析 把原方程转化为(x-1)-2$\sqrt{x-1}$+1+y+2-4$\sqrt{y+2}$+4+z+1-8$\sqrt{z+1}$+16=0,进一步利用完全平方公式和非负数的性质解答即可.
解答 解:∵x+y+z-2$\sqrt{x-1}$-4$\sqrt{y+2}$-8$\sqrt{z+1}$+23=0,
∴(x-1)-2$\sqrt{x-1}$+1+y+2-4$\sqrt{y+2}$+4+z+1-8$\sqrt{z+1}$+16=0,
∴($\sqrt{x-1}$-1)2+($\sqrt{y+2}$-2)2+($\sqrt{z+1}$-4)2=0,
∴$\sqrt{x-1}$=1,$\sqrt{y+2}$=2,$\sqrt{z+1}$=4,
∴x=2,y=2,z=15.
点评 此题考查配方法的运用,非负数的性质,利用完全平方公式因式分解是解决问题的关键.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | ||
| C. | 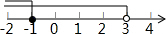 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,连接A、B两地间的高速公路全长为120千米,在AB上建有两个收费站C,D,已知AC:CB=1:5,AD:DB=11:1,一辆小车从C站到D站行驶了$\frac{3}{4}$小时,则小车的速度是每小时120千米.
如图,连接A、B两地间的高速公路全长为120千米,在AB上建有两个收费站C,D,已知AC:CB=1:5,AD:DB=11:1,一辆小车从C站到D站行驶了$\frac{3}{4}$小时,则小车的速度是每小时120千米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
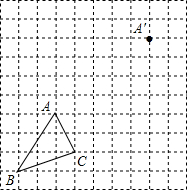 如图,在边长为1个单位长度的小正方形组成的网格中.
如图,在边长为1个单位长度的小正方形组成的网格中.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com