
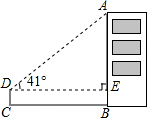
 如图,某校教学兴趣小组为测量建筑物AB的高度,用高度为1m的测量仪器CD,在距建筑物AB底部25m的C处,测得该建筑物顶部A处的仰角为∠ADE=41°,求建筑物AB的高度.(精确到0.1m).
如图,某校教学兴趣小组为测量建筑物AB的高度,用高度为1m的测量仪器CD,在距建筑物AB底部25m的C处,测得该建筑物顶部A处的仰角为∠ADE=41°,求建筑物AB的高度.(精确到0.1m). 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
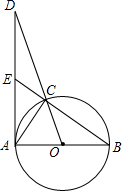 如图,已知AB是⊙O的直径,点C为圆上一点,点D在OC的延长线上,连接DA,交BC的延长线于点E,使得∠DAC=∠B.
如图,已知AB是⊙O的直径,点C为圆上一点,点D在OC的延长线上,连接DA,交BC的延长线于点E,使得∠DAC=∠B.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
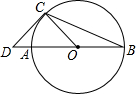 如图,AB是⊙O的直径,BC是弦,连结OC,过点C的切线交BA的延长线于点D,若OC=CD=2,则$\widehat{BC}$的长是$\frac{3π}{2}$.(结果保留π)
如图,AB是⊙O的直径,BC是弦,连结OC,过点C的切线交BA的延长线于点D,若OC=CD=2,则$\widehat{BC}$的长是$\frac{3π}{2}$.(结果保留π)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,反比例函数y=$\frac{6}{x}$(x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E,则下列结论正确的是(1)、(2)、(4)(将正确的结论填在横线上).
如图,反比例函数y=$\frac{6}{x}$(x>0)的图象经过矩形OABC对角线的交点M,分别与AB、BC相交于点D、E,则下列结论正确的是(1)、(2)、(4)(将正确的结论填在横线上).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
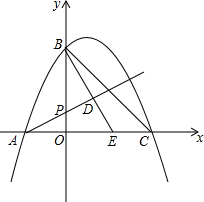 已知在平面直角坐标系xOy(如图)中,抛物线y=-x2+bx+c与x轴交于点A(-1,0)与点C(3,0),与y轴交于点B,点P为OB上一点,过点B作射线AP的垂线,垂足为点D,射线BD交x轴于点E.
已知在平面直角坐标系xOy(如图)中,抛物线y=-x2+bx+c与x轴交于点A(-1,0)与点C(3,0),与y轴交于点B,点P为OB上一点,过点B作射线AP的垂线,垂足为点D,射线BD交x轴于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com