
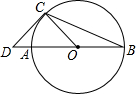
 如图,AB是⊙O的直径,BC是弦,连结OC,过点C的切线交BA的延长线于点D,若OC=CD=2,则$\widehat{BC}$的长是$\frac{3π}{2}$.(结果保留π)
如图,AB是⊙O的直径,BC是弦,连结OC,过点C的切线交BA的延长线于点D,若OC=CD=2,则$\widehat{BC}$的长是$\frac{3π}{2}$.(结果保留π) 科目:初中数学 来源: 题型:解答题
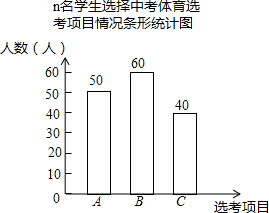 在学期初,某校体育组随机抽取了n名本校九年级学生,对这些学生选择中考体育选考项目进行问卷调查,问卷中的长春市中考体育选考项目包括:
在学期初,某校体育组随机抽取了n名本校九年级学生,对这些学生选择中考体育选考项目进行问卷调查,问卷中的长春市中考体育选考项目包括:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 长度相等的两条弧是等弧 | |
| B. | 顺次连结平行四边形四边中点所组成的图形是菱形 | |
| C. | 正八边形既是轴对称图形又是中心对称图形 | |
| D. | 三角形的内心到这个三角形三个顶点的距离相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
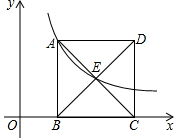 如图,正方形ABCD的边长为4,边BC在x轴上,点E是对角线AC,BD的交点,反比例函数y=$\frac{k}{x}(x>0)$的图象经过A,E两点,则k的值为( )
如图,正方形ABCD的边长为4,边BC在x轴上,点E是对角线AC,BD的交点,反比例函数y=$\frac{k}{x}(x>0)$的图象经过A,E两点,则k的值为( )| A. | 8 | B. | 4 | C. | 6 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
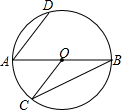 如图,AB是⊙O的直径,点C在圆周上,连结BC、OC,过点A作AD∥OC交⊙O于点D,若∠B=25°,则∠BAD的度数是( )
如图,AB是⊙O的直径,点C在圆周上,连结BC、OC,过点A作AD∥OC交⊙O于点D,若∠B=25°,则∠BAD的度数是( )| A. | 25° | B. | 30° | C. | 40° | D. | 50° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
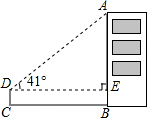 如图,某校教学兴趣小组为测量建筑物AB的高度,用高度为1m的测量仪器CD,在距建筑物AB底部25m的C处,测得该建筑物顶部A处的仰角为∠ADE=41°,求建筑物AB的高度.(精确到0.1m).
如图,某校教学兴趣小组为测量建筑物AB的高度,用高度为1m的测量仪器CD,在距建筑物AB底部25m的C处,测得该建筑物顶部A处的仰角为∠ADE=41°,求建筑物AB的高度.(精确到0.1m).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,为了测量教学楼前一棵大树的高度,王明和王亮拿自制的测倾器分别在教学楼AH的二楼C处测得树顶E的仰角为30°,在四楼B处测得大树底部D点的俯角为45°.已知二楼C处离地面高4米,四楼B处离地面高12米.试求树高DE.(参考数据:$\sqrt{3}$≈1.73,结果保留一位小数)
如图,为了测量教学楼前一棵大树的高度,王明和王亮拿自制的测倾器分别在教学楼AH的二楼C处测得树顶E的仰角为30°,在四楼B处测得大树底部D点的俯角为45°.已知二楼C处离地面高4米,四楼B处离地面高12米.试求树高DE.(参考数据:$\sqrt{3}$≈1.73,结果保留一位小数)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com