Question

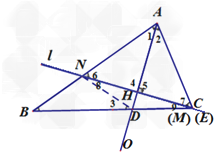
【题目】如图1，在△ABC中，∠ACB=2∠B，∠BAC的平分线AO交BC于点D，点H为AO上一动点，过点H作直线l⊥AO于H，分别交直线AB、AC、BC、于点N、E、M．

（1）当直线l经过点C时（如图2），求证：BN=CD；

（2）当M是BC中点时，写出CE和CD之间的等量关系，并加以证明；

（3）请直接写出BN、CE、CD之间的等量关系．

Answer 1

【答案】（1）证明见解析；（2）CD=2CE；（3）当点M 在线段BC 上时，CD=BN+CE ； 当点M 在BC 的延长线上时，CD=BN-CE ； 当点M 在CB 的延长线上时，CD=CE-BN.

【解析】试题分析：（1）连接ND，先由已知条件证明：DN=DC，再证明BN=DN即可；

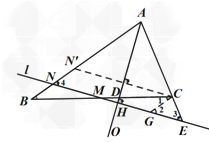
（2）当M是BC中点时，CE和CD之间的等量关系为CD=2CE，过点C作CN'⊥AO交AB于N'．过点C作CG∥AB交直线l于G，再证明△BNM≌△CGM问题得证；

（3）BN、CE、CD之间的等量关系要分三种情况讨论：①当点M在线段BC上时；②当点M在BC的延长线上时；③当点M在CB的延长线上时．

试题解析：（1 ）证明：连接ND ，

∵AO 平分∠BAC ， ∴∠1= ∠2 ，

∵直线l ⊥AO 于H ， ∴∠4= ∠5=90 °， ∴∠6= ∠7 ， ∴AN=AC ，

∴NH=CH ， ∴AH 是线段NC 的中垂线，∴DN=DC ，∴∠8= ∠9 ，∴∠AND= ∠ACB ，

∵∠AND= ∠B+ ∠3 ，∠ACB=2 ∠B ， ∴∠B= ∠3 ， ∴BN=DN ， ∴BN=DC ；

（2 ）如图，当M 是BC 中点时，CE 和CD 之间的等量关系为CD=2CE.

证明：过点C 作CN' ⊥AO 交AB 于N' ，

由（1 ）可得BN'=CD ，AN'=AC ，AN=AE ，∴∠4= ∠3 ，NN'=CE ，

过点C 作CG ∥AB 交直线l 于G ，∴∠4= ∠2 ，∠B= ∠1 ，∴∠2= ∠3 ，∴CG=CE ，

∵M 是BC 中点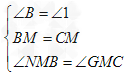， ，∴BM=CM ，

∴在△BNM 和△CGM 中，△BNM ≌△CGM ， ∴BN=CG ，∴BN=CE ，

∴CD=BN'=NN'+BN=2CE ；

（3 ）BN 、CE 、CD 之间的等量关系：

当点M 在线段BC 上时，CD=BN+CE ；

当点M 在BC 的延长线上时，CD=BN-CE ；

当点M 在CB 的延长线上时，CD=CE-BN.