
【题目】(1)如图甲,点O在直线AB上,OC 平分∠AOD,∠BOD= 42°12′,求∠AOC的度数.
(2)已知,如图乙,B、C 两点把线段AD 分成2:5:3三部分,M为AD的中点,BM=6cm,求CM和AD的长.

【答案】(1)68°54′;(2)4,20
【解析】
(1)根据题意找出这几个角之间的关系,利用角平分线的性质来求.
(2)由已知B,C两点把线段AD分成2:5:3三部分,所以设AB=2xcm,BC=5xcm,CD=3xcm,根据已知分别用x表示出AD,MD,从而得出BM,继而求出x,则求出CM和AD的长.
解:(1)∵∠AOB=180°,
∴∠AOD=180°-∠BOD=180°-42°12′=137°48′,
∵OC平分∠AOD,
∴∠AOC=![]() ∠AOD=
∠AOD=![]() ×137°48′=68°54′.
×137°48′=68°54′.
(2)设AB=2xcm,BC=5xcm,CD=3xcm
∴AD=AB+BC+CD=10xcm
∵M是AD的中点
∴AM=MD=![]() AD=5xcm
AD=5xcm
∴BM=AM-AB=5x-2x=3xcm
∵BM=6cm,
∴3x=6,x=2
故CM=MD-CD=5x-3x=2x=2×2=4cm,
AD=10x=10×2=20cm.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,用三个同(1)图的长方形和两个同(2)图的长方形用两种方式去覆盖一个大的长方形![]() ,两种方式为覆盖的部分(阴影部分)的周长一样,那么(1)图中长方形的面积
,两种方式为覆盖的部分(阴影部分)的周长一样,那么(1)图中长方形的面积![]() 与(2)图长方形的面积
与(2)图长方形的面积![]() 的比是( )
的比是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC=a.作BC边的三等分点C1,使得CC1∶BC1=1∶2,过点C1作AC的平行线交AB于点A1,过点A1作BC的平行线交AC于点D1,作BC1边的三等分点C2,使得C1C2∶BC2=1∶2,过点C2作AC的平行线交AB于点A2,过点A2作BC的平行线交A1C1于点D2;如此进行下去,则线段AnDn的长度为( )

A. ![]() aB.
aB. ![]() aC.
aC. ![]() aD.
aD. ![]() a
a
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种水彩笔,在购买时,若同时额外购买笔芯,每个优惠价为3元,使用期间,若备用笔芯不足时需另外购买,每个5元.现要对在购买水彩笔时应同时购买几个笔芯作出选择,为此收集了这种水彩笔在使用期内需要更换笔芯个数的30组数据.
水笔支数 | 4 | 6 | 8 | 7 | 5 |
需要更换的笔芯个数x | 7 | 8 | 9 | 10 | 11 |
设x表示水彩笔在使用期内需要更换的笔芯个数,y表示每支水彩笔在购买笔芯上所需要的费用(单位:元),n表示购买水彩笔的同时购买的笔芯个数.
(1)若x=9,n=7,则y= ;若x=7,n=9,则y= ;
(2)若n=9,用含x的的代数式表示y的取值;
(3)假设这30支笔在购买时,每支笔同时购买9个笔芯,或每支笔同时购买10个笔芯,分别计算这30支笔在购买笔芯时所需的费用,以费用最省作为选择依据,判断购买一支水彩笔的同时应购买9个还是10个笔芯?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB=3,AC=4,BC=5,P 为边 BC 上一动点,PE⊥AB 于 E,PF⊥AC于 F,M 为 EF 中点,则 AM 的最小值为( )

A.1B.1.3C.1.2D.1.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在直角梯形ABCD中,动点P从B点出发,沿B→C→D→A匀速运动,设点P运动的路程为x,△ABP的面积为y,图象如图2所示.
(1)在这个变化中,自变量、因变量分别是 、 ;
(2)当点P运动的路程x=4时,△ABP的面积为y= ;
(3)求AB的长和梯形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
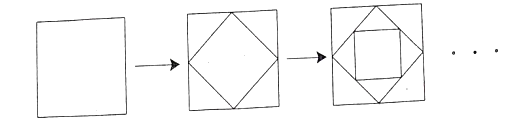
【题目】如图,依次连接边长为1的小正方形各边的中点,得到第二个小正方形,再依次连接第二个小正方形各边的中点得到第三个小正方形,按这样的规律第2019个小正方形的面积为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=1,BC=2,点E在AD上,且ED=2AE.
(1)求证:△ABC∽△EAB.
(2)AC与BE交于点H,求HC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:任意两个数a,b,按规则c=![]() a+b得到一个新数c,称所得的新数c为数a,b的“传承数。”
a+b得到一个新数c,称所得的新数c为数a,b的“传承数。”
(1)若a=1,b=2,求a,b的“传承数”c;
(2)若a=1,b=![]() ,且
,且![]() +3x+1=0,求a,b的“传承数”c;
+3x+1=0,求a,b的“传承数”c;
(3)若a=2n+1,b=n1,且a,b的“传承数”c值为一个整数,则整数n的值是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com