
【题目】如图,在矩形ABCD中,AB=1,BC=2,点E在AD上,且ED=2AE.
(1)求证:△ABC∽△EAB.
(2)AC与BE交于点H,求HC的长.

【答案】(1)证明见解析;(2)HC=![]() .
.
【解析】试题分析:(1)、根据矩形的性质得出AB=CD=1,BC=AD=2,∠ABC=∠BAD=90°,根据ED=3AE得出AE=![]() ,ED=
,ED=![]() ,从而得到
,从而得到![]() ,然后结合公共角得出三角形相似;(2)、根据三角形相似得出∠BHC=90°,根据Rt△ABC的面积相等得出BH的长度,然后根据Rt△BHC的勾股定理求出CH的长度.
,然后结合公共角得出三角形相似;(2)、根据三角形相似得出∠BHC=90°,根据Rt△ABC的面积相等得出BH的长度,然后根据Rt△BHC的勾股定理求出CH的长度.
试题解析:(1)、证明:∵四边形ABCD是矩形,∴AB=CD=1,BC=AD=2,∠ABC=∠BAD=90°,
∴ED=3AE,∴AE=![]() ,ED=
,ED=![]() ∵
∵![]() ,∴
,∴![]() ,
,
∵∠ABC=∠BAE=90°,∴△ABC∽△EAB
(2)、∵△ABC∽△EAB,∴∠ACB=∠ABE,∵∠ABE+∠CBH=90°,∴∠ACB+∠CBE=90°,∴∠BHC=90° ∴BH⊥AC
在Rt△ACB中,∵∠ABC=90°,AB=1,BC=2,∴AC=![]() ,∵
,∵![]() ∴BH=
∴BH=![]() ,
,
∴CH=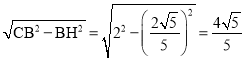 .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】我市某外资企业生产的一批产品上市后30天内全部售完,该企业对这批产品上市后每天的销售情况进行了跟踪调查.其中,国内市场的日销售量y1(万件)与时间t(t为整数,单位:天)的部分对应值如下表所示.而国外市场的日销售量y2(万件)与时间t(t为整数,单位:天)的关系如图所示.

(1)请你从所学过的一次函数、二次函数和反比例函数中确定哪种函数能表示y1与t的变化规律,写出y1与t的函数关系式及自变量t的取值范围;
(2)分别探求该产品在国外市场上市20天前(不含第20天)与20天后(含第20天)的日销售量y2与时间t所符合的函数关系式,并写出相应自变量t的取值范围;
(3)设国内、外市场的日销售总量为y万件,写出y与时间t的函数关系式,并判断上市第几天国内、外市场的日销售总量y最大,并求出此时的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂生产一种合金薄板(其厚度忽略不计)这些薄板的形状均为正方形,边长(单位:cm)在5~50之间,每张薄板的成本价(单位:元)与它的面积(单位:cm2)成正比例,每张薄板的出厂价(单位:元)由基础价和浮动价两部分组成,(即出厂价=基础价+浮动价)其中基础价与薄板的大小无关,是固定不变的,浮动价与薄板的边长x成正比例,在营销过程中得到了表格中的数据,已知出厂一张边长为40cm的薄板,获得利润是26元.(利润=出厂价-成本价)
薄板的边长(cm) | 20 | 30 |
出厂价(元/张) | 50 | 70 |
(1)求一张薄板的出厂价y与边长x之间满足的函数关系式;
(2)求一张薄板的利润p与边长x之间的函数关系式;
(3)若一张薄板的利润是34元,且成本最低,此时薄板的边长为多少?当薄板的边长为多少时,所获利润最大,求出这个最大值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,ABC的顶点都在格点上,在平面直角坐标系。

⑴写出点的坐标:点A ,点B ,点C .
⑵将ABC向右平移7个单位,再向下平移3个单位,得到A1B1C1,试在图上画出A1B1C1的图形;
⑶求ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实党中央提出的“惠民政策”,我市今年计划开发建设A、B两种户型的“廉租房”共40套.投入资金不低于270万元,又不超过296万元.开发建设办公室预算:一套A型“廉租房”的造价为10万元,一套B型“廉租房”的造价为4.8万元.
(1)请问有几种开发建设方案?
(2) 在投入资金最少的方案下,为了让更多的人享受到“惠民”政策,开发建设办公室决定通过缩小“廉租房”的面积来降低造价、节省资金.每套A户型“廉租房”的造价降低1万元,每套B户型“廉租房”的造价降低0.3万元,将节省下来的资金全部用于再次开发建设缩小面积后的“廉租房”,如果同时建设A、B两种户型,请你直接写出再次开发建设的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位招聘员工,采取笔试与面试相结合的方式,两项成绩的原始分均为100分,前6名选手的得分如下:

根据规定,笔试成绩和面试成绩按一定的百分比折合成综合成绩(综合成绩的满分仍为100分)
(1)这6名选手笔试成绩的平均数是_____分,中位数是_____分,众数是______分.
(2)现已知1号选手的综合成绩为88分,求笔试成绩和面试成绩的百分比各为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AC是⊙O的直径,点B在圆周上(不与A、C重合),点D在AC的延长线上,连接BD交⊙O于点E,若∠AOB=3∠ADB,则( )

A. DE=EB B. ![]() DE=EB C.
DE=EB C. ![]() DE=DO D. DE=OB
DE=DO D. DE=OB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在解不等式|x+1|>2时,我们可以采用下面的解答方法:
①当x+1≥0时,|x+1|=x+1.
∴由原不等式得x+1>2.∴可得不等式组![]()
∴解得不等式组的解集为x>1.
②当x+1<0时,|x+1|=﹣(x+1).
∴由原不等式得﹣(x+1)>2.∴可得不等式组![]()
∴解得不等式组的解集为x<﹣3.
综上所述,原不等式的解集为x>1或x<﹣3.
请你仿照上述方法,尝试解不等式|x﹣2|≤1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是我市某一天内的气温变化图,根据图象,下列说法中错误的是( )

A.这一天中最高气温是26℃
B.这一天中最高气温与最低气温的差为16℃
C.这一天中2时至14时之间的气温在逐渐升高
D.这一天中14时至24时之间的气温在逐渐降低
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com