
【题目】已知抛物线y=ax2﹣bx.
(1)若此抛物线与直线y=x只有一个公共点,且向右平移1个单位长度后,刚好过点(3,0).
①求此抛物线的解析式;
②以y轴上的点P(0,n)为中心,作该抛物线关于点P对称的抛物线y',若这两条抛物线有公共点,求n的取值范围;
(2)若a>0,将此抛物线向上平移c个单位(c>0),当x=c时,y=0;当0<x<c时,y>0.试比较ac与1的大小,并说明理由.
【答案】(1)①![]() ;②n≤0;(2)ac≤1,见解析.
;②n≤0;(2)ac≤1,见解析.
【解析】
(1)①△=0求解b=1,将点(3,0)代入平移后解析式,即可;
②顶点为(1,![]() )关于P(0,n)对称点的坐标是(﹣1,2n﹣
)关于P(0,n)对称点的坐标是(﹣1,2n﹣![]() ),关于点P中心对称的新抛物线y'=
),关于点P中心对称的新抛物线y'=![]() (x+1)2+2n﹣
(x+1)2+2n﹣![]() =
=![]() x2+x+2n,联立方程组即可求n的范围;
x2+x+2n,联立方程组即可求n的范围;
(2)将点(c,0)代入y=ax2﹣bx+c得到ac﹣b+1=0,b=ac+1,当0<x<c时,y>0. ![]() ≥c,b≥2ac,ac+1≥2ac,ac≥1;
≥c,b≥2ac,ac+1≥2ac,ac≥1;
解:(1)①ax2﹣bx=x,ax2﹣(b+1)x=0,
△=(b+1)2=0,b=﹣1,
平移后的抛物线y=a(x﹣1)2﹣b(x﹣1)过点(3,0),
∴4a﹣2b=0,
∴a=﹣![]() ,b=﹣1,
,b=﹣1,
原抛物线:y=﹣![]() x2+x,
x2+x,
②其顶点为(1,![]() )关于P(0,n)对称点的坐标是(﹣1,2n﹣
)关于P(0,n)对称点的坐标是(﹣1,2n﹣![]() ),
),
∴关于点P中心对称的新抛物线y'=![]() (x+1)2+2n﹣
(x+1)2+2n﹣![]() =
=![]() x2+x+2n.
x2+x+2n.
由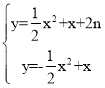 得:x2+2n=0有解,所以n≤0.
得:x2+2n=0有解,所以n≤0.
(2)由题知:a>0,将此抛物线y=ax2﹣bx向上平移c个单位(c>0),
其解析式为:y=ax2﹣bx+c过点(c,0),
∴ac2﹣bc+c=0 (c>0),
∴ac﹣b+1=0,b=ac+1,
且当x=0时,y=c,
对称轴:x=![]() ,抛物线开口向上,画草图如右所示.
,抛物线开口向上,画草图如右所示.
由题知,当0<x<c时,y>0.
∴![]() ≥c,b≥2ac,
≥c,b≥2ac,
∴ac+1≥2ac,ac≤1;


科目:初中数学 来源: 题型:
【题目】数学课上,潘老师给出如下定义:如果一个三角形有一边上的高线等于这条边的一半,那么称这个三角形为“垂美三角形”,这条边称为这个三角形的“垂美边”.
概念理解:
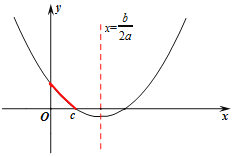
(1)如图①,已知∠A=90°,AB=AC,请证明等腰Rt△ABC一定是“垂美三角形”.
探索运用:
(2)已知等腰△ABC是“垂美三角形”,请求出顶角的度数.
能力提升:
(3)如图②,在直角坐标系中,点A为x轴正半轴上动点,在反比例函数![]() 的图象上是否存在点B,使△OAB是“垂美三角形”,且OA,OB均为“垂美边”,若存在,请求出点B的坐标.
的图象上是否存在点B,使△OAB是“垂美三角形”,且OA,OB均为“垂美边”,若存在,请求出点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大学生自主创业,集资5万元开品牌专卖店,已知该品牌商品成本为每件a元,市场调查发现日销售量y(件)与销售价x(元/件)之间存在一次函数关系如表:
销售价x(元/件) | … | 110 | 115 | 120 | 125 | 130 | … |
销售量y(件) | … | 50 | 45 | 40 | 35 | 30 | … |
若该店某天的销售价定为110元/件,雇有3名员工,则当天正好收支平衡(其中支出=商品成本+员工工资+应支付其它费用):已知员工的工资为每人每天100元,每天还应支付其它费用为200元(不包括集资款).
(1)求日销售量y(件)与销售价x(元/件)之间的函数关系式;
(2)该店现有2名员工,试求每件服装的销售价定为多少元时,该服装店每天的毛利润最大:(毛利润═销售收入一商品成本一员工工资一应支付其他费用)
(3)在(2)的条件下,若每天毛利润全部积累用于一次性还款,而集资款每天应按其万分之二的利率支付利息,则该店最少需要多少天(取整数)才能还清集资款?
查看答案和解析>>
科目:初中数学 来源: 题型:
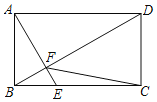
【题目】如图,在矩形ABCD中,点E是BC边上的一点,且AE⊥BD,垂足为点F,∠DAE=2∠BAE.
(1)求证:BF:DF=1:3;
(2)若四边形EFDC的面积为11,求△CEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班要在一面墙上同时展示数张形状、大小均相同的矩形绘画作品,将这些作品排成一个矩形(作品不完全重合).现需要在每张作品的四个角落都钉上图钉,如果作品有角落相邻,那么相邻的角落共享一枚图钉(例如用9枚图钉将4张作品钉在墙上如图).若有28枚图钉可供选用,则最多可以展示绘画作品( )
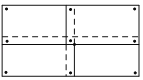
A. 16张B. 18张C. 20张D. 21张
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字
,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字![]() ,
,![]() ,
,![]() ,
,![]() ,如图
,如图![]() ,正方形
,正方形![]() 顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.如:若从图
顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.如:若从图![]() 起跳,第一次掷得
起跳,第一次掷得![]() ,就顺时针连续跳
,就顺时针连续跳![]() 个边长,落到圈
个边长,落到圈![]() ;若第二次掷得
;若第二次掷得![]() ,就从
,就从![]() 开始顺时针连续跳
开始顺时针连续跳![]() 个边长,落到圈
个边长,落到圈![]() ;
;![]() 设游戏者从圈
设游戏者从圈![]() 起跳.
起跳.
(![]() )嘉嘉随机掷一次骰子,求落回到圈
)嘉嘉随机掷一次骰子,求落回到圈![]() 的概率
的概率![]() .
.
(![]() )淇淇随机掷两次骰子,用列表法求最后落回到圈
)淇淇随机掷两次骰子,用列表法求最后落回到圈![]() 的概率
的概率![]() ,并指出她与嘉嘉落回到圈
,并指出她与嘉嘉落回到圈![]() 的可能性一样吗?
的可能性一样吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某青春党支部在精准扶贫活动中,给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种.已知乙种树苗的价格比甲种树苗贵10元,用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同.
(1)求甲、乙两种树苗每棵的价格各是多少元?
(2)在实际帮扶中,他们决定再次购买甲、乙两种树苗共50棵,此时,甲种树苗的售价比第一次购买时降低了10%,乙种树苗的售价不变,如果再次购买两种树苗的总费用不超过1500元,那么他们最多可购买多少棵乙种树苗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB 为半⊙O 的直径,弦 AC 的延长线与过点 B 的切线交于点 D,E 为 BD的中点,连接 CE.
(1)求证:CE 为 O 的切线;
(2)过点 C 作 CF AB ,垂足为点 F,AC=5,CF=3,求⊙O的半径.
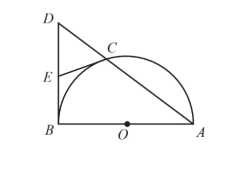
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB是半圆O的直径,AC是弦,点P沿BA方向,从点B运动到点A,速度为1cm/s,若AB=10cm,点O到AC的距离为4cm.
(1)求弦AC的长;
(2)问经过多长时间后,△APC是等腰三角形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com