
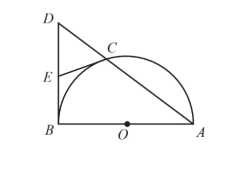
【题目】如图,AB 为半⊙O 的直径,弦 AC 的延长线与过点 B 的切线交于点 D,E 为 BD的中点,连接 CE.
(1)求证:CE 为 O 的切线;
(2)过点 C 作 CF AB ,垂足为点 F,AC=5,CF=3,求⊙O的半径.
科目:初中数学 来源: 题型:
【题目】某商场开展购物抽奖活动,抽奖箱中有3个形状、大小和质地等完全相同的小球,分别标有数字1、2、3.顾客从中随机摸出一个小球,然后放回箱中,再随机摸出一个小球.
(1)利用树形图法或列表法(只选其中一种),表示摸出小球可能出现的所有结果;
(2)若规定:两次摸出的小球的数字之积为9,则为一等奖;数字之积为6,则为二等奖;数字之积为2或4,则为三等奖.请你分别求出顾客抽中一等奖、二等奖、三等奖的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
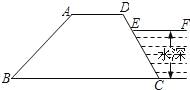
【题目】有一水库大坝的横截面是梯形ABCD,AD∥BC,EF为水库的水面,点E在DC上,某课题小组在老师的带领下想测量水的深度,他们测得背水坡AB的长为12米,迎水坡上DE的长为2米,∠BAD=135°,∠ADC=120°,求水深.(精确到0.1米,![]() =1.41,
=1.41,![]() =1.73)
=1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由边长为1的小正方形组成的10×5网格,每个小正方形的顶点叫做格点,点A,B,C,D均在格点上,在网格中将点B按下列步骤移动第一步:点B绕点A逆时针旋转180°得到点B1;第二步:点B1绕点D逆时针旋转90°得到点B2;第三步:点B2绕点C逆时针旋转90°回到点B
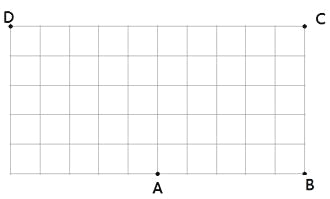
(1)请用圆规画出点B→B1→B2→B经过的路径;
(2)所画图形是_______图形;
(3)求所画图形的周长(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝重庆南开中学建校83周年暨校运动会,我校初二(21)班准备统一穿初一时期订制的服装参加运动会,分别需要增订“英伦学院风”班服(250元/件)、“![]() ”运动裤(90元/件)、“少年的我”短袖
”运动裤(90元/件)、“少年的我”短袖![]() 恤(40元/件)共50件(三种服装均有增订),总花费6000元,且需要增订“少年的我”短袖
恤(40元/件)共50件(三种服装均有增订),总花费6000元,且需要增订“少年的我”短袖![]() 恤的件数最多,则需要增订“
恤的件数最多,则需要增订“![]() ”运动裤__________件.
”运动裤__________件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E.
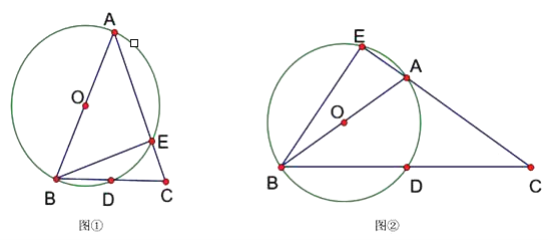
(1)当∠BAC为锐角时,如图①,求证:∠CBE=![]() ∠BAC;
∠BAC;
(2)当∠BAC为钝角时,如图②,CA的延长线与⊙O相交于点E,(1)中的结论是否仍然成立?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校数学兴趣小组,对函数y=|x﹣1|+1的图象和性质进行了探究,探究过程如下:
(1)自变量x的取值范围是全体实数,x与y的几组对应值如表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 5 | 4 | m | 2 | 1 | 2 | 3 | 4 | 5 | … |
其中m= .
(2)如图,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象:
(3)根据画出的函数图象特征,仿照示例,完成下列表格中的函数变化规律:
序号 | 函数图象特征 | 函数变化规律 |
示例1 | 在直线x=1的右侧,函数图象呈上升状态 | 当x>1时,y随x的增大而增大 |
① | 在直线x=1的左侧,函数图象呈下降状态 |
|
示例2 | 函数图象经过点(﹣3,5) | 当x=﹣3时,y=5 |
② | 函数图象的最低点是(1,1) |
|
(4)当2<y≤4时,x的取值范围为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为宣传6月6日世界海洋日,某校八年级举行了主题为“珍惜海洋资源,保护海洋生物多样性”的知识竞赛活动.为了解全年级500名学生此次竞赛成绩(百分制)的情况,随机抽取了部分参赛学生的成绩,整理并绘制出如下不完整的统计表(表1)和统计图(如图).请根据图表信息解答以下问题:

(1)本次调查一共随机抽取了个参赛学生的成绩;
(2)表1中a= ;
(3)所抽取的参赛学生的成绩的中位数落在的“组别”是 ;
(4)请你估计,该校九年级竞赛成绩达到90分以上(含90分)的学生约有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有![]() 个大小、质地都相同的乒乓球,球面上分别标有数字
个大小、质地都相同的乒乓球,球面上分别标有数字![]() 、
、![]() 、
、![]() 、
、![]() ,搅匀后先从中摸出一个球(不放回),再从余下的
,搅匀后先从中摸出一个球(不放回),再从余下的![]() 个球中摸出
个球中摸出![]() 个球.
个球.
(1)用树状图列出所有可能出现的结果;
(2)求![]() 次摸出的乒乓球球面上数字的积为偶数的概率.
次摸出的乒乓球球面上数字的积为偶数的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com