
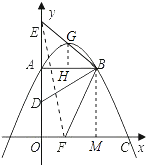
����Ŀ����ͼ����ֱ֪������OABC�ı�OA��y����������ϣ�OC��x����������ϣ�OA=AB=2��OC=3������B��BD��BC����OA�ڵ�D������DBC�Ƶ�B��˳ʱ�뷽����ת���ǵ����߷ֱ�y��������ᡢx�����������E��F��
��1����A��B��C����������ߵĽ���ʽ��
��2����BE������1���������ߵĶ���ʱ����CF�ij���
��3������EF�����BEF���BFC�����֮��ΪS���ʣ���CFΪ��ֵʱS��С������������Сֵ��
���𰸡�
��1��
�⣺������ɵ�A��0��2����B��2��2����C��3��0����
�����������ߵĽ���ʽΪy=ax2+bx+c��a��0����
�� 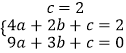 ��
��
��� 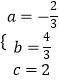 ��
��
�������ߵĽ���ʽΪy=�� ![]() +
+ ![]() x+2
x+2
��2��
�⣺�������ߵĶ���ΪG��
��G��1�� ![]() ��������G��GH��AB������ΪH��
��������G��GH��AB������ΪH��
��AH=BH=1��GH= ![]() ��2=
��2= ![]() ��
��
��EA��AB��GH��AB��
��EA��GH��
��GH�ǡ�BEA����λ�ߣ�
��EA=2GH= ![]() ��
��
����B��BM��OC������ΪM����BM=OA=AB��
�ߡ�EBF=��ABM=90�㣬
���EBA=��FBM=90�㩁��ABF��
��Rt��EBA��Rt��FBM��
��FM=EA= ![]() ��
��
��CM=OC��OM=3��2=1��
��CF=FM+CM= ![]()
��3��
�⣺��CF=a����FM=a��1��
��BF2=FM2+BM2=��a��1��2+22=a2��2a+5��
�ߡ�EBA�ա�FBM��
��BE=BF��
��S��BEF= ![]() BEBF=
BEBF= ![]() ��a2��2a+5����
��a2��2a+5����
�֡�S��BFC= ![]() FCBM=
FCBM= ![]() ��a��2=a��
��a��2=a��
��S= ![]() ��a2��2a+5����a=
��a2��2a+5����a= ![]() a2��2a+
a2��2a+ ![]() ��
��
��S= ![]() ��a��2��2+
��a��2��2+ ![]() ��
��
�൱a=2����0��a��3��Χ�ڣ�ʱ��S��Сֵ= ![]() ��
��
����������1������OA��AB��OC�ij������ɵõ�A��B��C��������꣬�������ô���ϵ������������ߵĽ���ʽ����2������Ҫͨ������ȫ����������⣻��B��BM��x����M�����ڡ�EBF���ɡ�DBC��ת���ã����������Ƕ���ֱ�ǣ���ô��EBF=��ABM=90�㣬����ͬ�ǵ������ȿɵá�EBA=��FBM����֪BM=OA=AB=2���ɴ˿�֤�á�FBM�ա�EBA����AE=FM��CM�ij�����ã��ؼ���FM��AE�ij����������ߵĶ���ΪG������G�����߶�AB�Ĵ�ֱƽ�����ϣ�����G��GH��AB����GH�ǡ�ABE����λ�ߣ�G�����������ã����ɵõ�GH�ij����Ӷ������AE�ij���������CF=CM+FM=AE+CM���CF�ij�����3���ɣ�2����ȫ����������֤��BE=BF�����BEF�ǵ���ֱ�������Σ������ΪBFƽ����һ�룻��BFC�У���CFΪ�ף�BMΪ���������BFC�����������CF�ij�Ϊa��������ʾ��FM�ij����ɹ��ɶ����������BF��ƽ���������ϵó������������ε�������㷽�������ɵõ�����S��a�ĺ�����ϵʽ�����ݺ��������ʼ������S����Сֵ����Ӧ��CF�ij���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˱�ս������������ѧʵ��������ԣ�ijУ�Գ���ѧ��������ģ��ѵ������������ѧ����4����ͬ�IJ���ʵ����Ŀ�������÷��Ţ١��ڡ��ۡ��ܴ�������ѧ����ĸa��b��c��d��ʾ������ʱÿ��ѧ��ÿ��ֻ����һ��ʵ�飬ʵ�����Ŀ��ѧ����ǩȷ������һ�γ�ǩȷ������ʵ����Ŀ���ڶ��γ�ǩȷ����ѧʵ����Ŀ��
��1����������ͼ�����б�������ʾij��ͬѧ��ǩ�ĸ��ֿ��������
��2��С��ͬѧ�������Ģ١��ںͻ�ѧ��b��c��ʵ�����ýϺã���ͬʱ�鵽���ƶ����ĽϺõ�ʵ����Ŀ�ĸ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�ڽ��ڡ�O��F�� ![]() ��һ�㣬��
��һ�㣬�� ![]() =
= ![]() ������CF���ӳ���AD���ӳ����ڵ�E������AC������ABC=105�㣬��BAC=25�㣬���E�Ķ���Ϊ�� ��
������CF���ӳ���AD���ӳ����ڵ�E������AC������ABC=105�㣬��BAC=25�㣬���E�Ķ���Ϊ�� �� 
A.45��
B.50��
C.55��
D.60��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y=ax2+bx+c��ͼ����x��Ľ���ΪA��D��A��D���Ҳࣩ����y��Ľ���ΪC����A��4��0����C��0����3�����Գ�����ֱ��x=1��
��1������κ����Ľ���ʽ��
��2����M�ǵ���������������һ���㣬�Һ�����Ϊm�����ı���OCMA�����Ϊs����д��s��m֮��ĺ�����ϵʽ���������mΪ��ֵʱ���ı���OCMA��������
��3�����B��x���ϵĵ㣬P���������ϵĵ㣬�Ƿ���ڵ�P��ʹ����A��B��C��P�ĵ�Ϊ������ı���Ϊƽ���ı��Σ������ڣ�ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ƽ��ֱ������ϵxOy�У�O������ԭ�㣬��A�Ǻ���y1= ![]() ��x��0��ͼ����һ�㣬AO���ӳ��߽�����y2=
��x��0��ͼ����һ�㣬AO���ӳ��߽�����y2= ![]() ��x��0��k��0����y2ͼ���ڵ�B��BC��x�ᣬ��S��ABC=
��x��0��k��0����y2ͼ���ڵ�B��BC��x�ᣬ��S��ABC= ![]() ������y2 ��
������y2 �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������и���
��1�����㣺����2��2�� ![]() ��1+tan45�㣩
��1+tan45�㣩
��2���Ȼ�������ֵ�� ![]() ������a=
������a= ![]() ��2��b=
��2��b= ![]() +2��
+2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2017���п���������ij���ƻ���4����Ѯ��ij���ܶ���������3������������ԣ�����ʦ������ʦ���������뵱���ʦ������ʦ���ѡ��2�죬����ʦ���ѡ��1�쵱���ʦ��
��1��������ʦѡ���ܶ�������������ĸ����Ƕ��٣�
��2��������ʦ������ʦ����ͬһ���������Եĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪����ABCD����������A����3��4����B����3��0����C����1��0������DΪ�����������y=ax2+bx+c����B������P�ӵ�D��������DC�����C�˶���ͬʱ����Q�ӵ�B��������BA�����A�˶�����P��Q�˶����ٶȾ�Ϊÿ��1����λ���˶���ʱ��Ϊt�룮����P��PE��CD��BD�ڵ�E������E��EF��AD�ڵ�F�����������ڵ�G��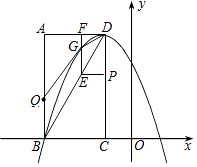
��1���������ߵĽ���ʽ��
��2����tΪ��ֵʱ���ı���BDGQ�����������ֵΪ���٣�
��3������P��Q�˶������У��ھ���ABCD�ڣ�������߽磩�Ƿ���ڵ�H��ʹ��B��Q��E��HΪ������ı��������Σ������ڣ���ֱ��д����ʱ���ε��ܳ����������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�ž���ֽƬ������ͼ������ ����ABE��BE���ۣ�ʹ��A���ڶԽ���BD�ϵ�M�㣬����CDF��DF���ۣ�ʹ��C���ڶԽ���BD�ϵ�N�㣮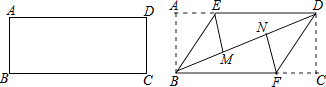
��1����֤���ı���BFDE��ƽ���ı��Σ�
��2�����ı���BFDE�����Σ�AB=2��������BFDE�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com