
【题目】如图,在平面直角坐标系中,已知矩形ABCD的三个顶点A(﹣3,4)、B(﹣3,0)、C(﹣1,0).以D为顶点的抛物线y=ax2+bx+c过点B.动点P从点D出发,沿DC边向点C运动,同时动点Q从点B出发,沿BA边向点A运动,点P、Q运动的速度均为每秒1个单位,运动的时间为t秒.过点P作PE⊥CD交BD于点E,过点E作EF⊥AD于点F,交抛物线于点G.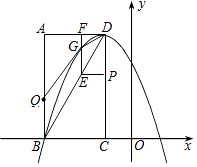
(1)求抛物线的解析式;
(2)当t为何值时,四边形BDGQ的面积最大?最大值为多少?
(3)动点P、Q运动过程中,在矩形ABCD内(包括其边界)是否存在点H,使以B,Q,E,H为顶点的四边形是菱形,若存在,请直接写出此时菱形的周长;若不存在,请说明理由.
【答案】
(1)
解:由题意得,顶点D点的坐标为(﹣1,4).
设抛物线的解析式为y=a (x+1)2+4(a≠0),
∵抛物线经过点B(﹣3,0),代入y=a (x+1)2+4
可求得a=﹣1
∴抛物线的解析式为y=﹣(x+1)2+4,即y=﹣x2﹣2x+3
(2)
解:由题意知,DP=BQ=t,
∵PE∥BC,
∴△DPE∽△DBC.
∴ ![]() =
= ![]() =2,
=2,
∴PE= ![]() DP=
DP= ![]() t.
t.
∴点E的横坐标为﹣1﹣ ![]() t,AF=2﹣
t,AF=2﹣ ![]() t.
t.
将x=﹣1﹣ ![]() t代入y=﹣(x+1)2+4,得y=﹣
t代入y=﹣(x+1)2+4,得y=﹣ ![]() t2+4.
t2+4.
∴点G的纵坐标为﹣ ![]() t2+4,
t2+4,
∴GE=﹣ ![]() t2+4﹣(4﹣t)=﹣
t2+4﹣(4﹣t)=﹣ ![]() t2+t.
t2+t.
如图1所示:连接BG.
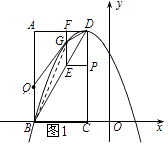
S四边形BDGQ=S△BQG+S△BEG+S△DEG,即S四边形BDGQ= ![]() BQAF+
BQAF+ ![]() EG(AF+DF)
EG(AF+DF)
= ![]() t(2﹣
t(2﹣ ![]() t)﹣
t)﹣ ![]() t2+t.
t2+t.
=﹣ ![]() t2+2t=﹣
t2+2t=﹣ ![]() (t﹣2)2+2.
(t﹣2)2+2.
∴当t=2时,四边形BDGQ的面积最大,最大值为2
(3)
解:存在.
∵CD=4,BC=2,
∴tan∠BDC= ![]() ,BD=2
,BD=2 ![]() .
.
∴cos∠BDC= ![]() .
.
∵BQ=DP=t,
∴DE= ![]() t.
t.
如图2所示:当BE和BQ为菱形的邻边时,BE=QB.
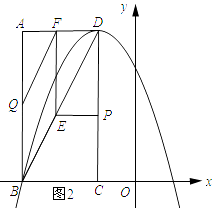
∵BE=BD﹣DE,
∴BQ=BD﹣DE,即t=2 ![]() ﹣
﹣ ![]() t,解得t=20﹣8
t,解得t=20﹣8 ![]() .
.
∴菱形BQEH的周长=80﹣32 ![]() .
.
如图3所示:当BE为菱形的对角时,则BQ=QE,过点Q作QM⊥BE,则BM=EM.
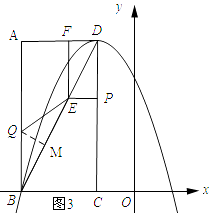
∵MB=cos∠QBMBQ,
∴MB= ![]() t.
t.
∴BE= ![]() t.
t.
∵BE+DE=BD,
∴ ![]() t+
t+ ![]() t=2
t=2 ![]() ,解得:t=
,解得:t= ![]() .
.
∴菱形BQEH的周长为 ![]() .
.
综上所述,菱形BQEH的周长为 ![]() 或80﹣32
或80﹣32 ![]()
【解析】(1)先求得点D的坐标,设抛物线的解析式为y=a (x+1)2+4(a≠0),将点B的坐标代入可求得a的值,故此可得到抛物线的解析式;(2)由题意知,DP=BQ=t,然后证明△DPE∽△DBC,可得到PE= ![]() t,然后可得到点E的横坐标(用含t的式子表示),接下来可求得点G的坐标,然后依据S四边形BDGQ=S△BQG+S△BEG+S△DEG , 列出四边形的面积与t的函数关系式,然后依据利用配方法求解即可;(3)首先用含t的式子表示出DE的长,当BE和BQ为菱形的邻边时,由BE=QB可列出关于t的方程,从而可求得t的值,然后可求得菱形的周长;当BE为菱形的对角时,则BQ=QE,过点Q作QM⊥BE,则BM=EM.然后用含t的式子表示出BE的长,最后利用BE+ED=BD列方程求解即可.
t,然后可得到点E的横坐标(用含t的式子表示),接下来可求得点G的坐标,然后依据S四边形BDGQ=S△BQG+S△BEG+S△DEG , 列出四边形的面积与t的函数关系式,然后依据利用配方法求解即可;(3)首先用含t的式子表示出DE的长,当BE和BQ为菱形的邻边时,由BE=QB可列出关于t的方程,从而可求得t的值,然后可求得菱形的周长;当BE为菱形的对角时,则BQ=QE,过点Q作QM⊥BE,则BM=EM.然后用含t的式子表示出BE的长,最后利用BE+ED=BD列方程求解即可.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:初中数学 来源: 题型:
【题目】矩形、菱形、正方形都是平行四边形,但它们都是有特殊条件的平行四边形,正方形不仅是特殊的矩形,也是特殊的菱形.因此,我们可利用矩形、菱形的性质来研究正方形的有关问题.回答下列问题: 
(1)将平行四边形、矩形、菱形、正方形填入它们的包含关系的下图中.
(2)要证明一个四边形是正方形,可先证明四边形是矩形,再证明这个矩形的相等;或者先证明四边形是菱形,在证明这个菱形有一个角是 .
(3)某同学根据菱形面积计算公式推导出对角线长为a的正方形面积是S=0.5a2 , 对此结论,你认为是否正确?若正确,请说明理由;若不正确,请举出一个反例说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直角梯形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=AB=2,OC=3,过点B作BD⊥BC,交OA于点D.将∠DBC绕点B按顺时针方向旋转,角的两边分别交y轴的正半轴、x轴的正半轴于E和F.
(1)求经过A、B、C三点的抛物线的解析式;
(2)当BE经过(1)中抛物线的顶点时,求CF的长;
(3)连接EF,设△BEF与△BFC的面积之差为S,问:当CF为何值时S最小,并求出这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC与△A′B′C′都是等腰三角形,且AB=AC=5,A′B′=A′C′=3,若∠B+∠B′=90°,则△ABC与△A′B′C′的面积比为 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在8×8的正方形网格中,有一个Rt△AOB,点O是直角顶点,点O、A、B分别在网格中小正方形的顶点上,请按照下面要求在所给的网格中画图.
(1)在图1中,将△AOB先向右平移3个单位,再向上平移2个单位,得到△A1O1B1 , 画出平移后的△A1O1B1;(其中点A、O、B的对应点分别为点A1 , O1 , B1) 
(2)在图2中,△AOB与△A2O2B2是关于点P对称的图形,画出△A2O2B2 , 连接BA2 , 并直接写出tan∠A2BO的值.(其中A,O,B的对应点分别为点A2 , O2 , B2) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明早晨跑步,他从自己家出发,向东跑了2km到达小彬家,继续向东跑了1.5km到达小红家,然后又向西跑了4.5km到达学校,最后又向东,跑回到自己家.
(1)以小明家为原点,以向东为正方向,用1个单位长度表示1km,在图中的数轴上,分别用点A表示出小彬家,用点B表示出小红家,用点C表示出学校的位置;![]()
(2)求小彬家与学校之间的距离;
(3)如果小明跑步的速度是250m/min,那么小明跑步一共用了多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于F,且AF=BD,连接BF. 
(1)求证:D是BC的中点.
(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com