
【题目】2017年中考,阜阳市某区计划在4月中旬的某个周二至周四这3天进行理化加试.王老师和朱老师都将被邀请当监考老师,王老师随机选择2天,朱老师随机选择1天当监考老师.
(1)求王老师选择周二、周三这两天的概率是多少?
(2)求王老师和朱老师两人同一天监考理化加试的概率.
【答案】
(1)解:王老师选择的时间有以下3种可能:(2,3),(2,4),(3,4),
所以王老师选择周二,周三的概率是 ![]()
(2)解: 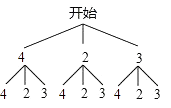
由树状图可知,共有9种等可能的结果,其中他们能同天监考的结果有6种,
∴他们同天监考的概率是 ![]() =
= ![]()
【解析】(1)用列举法得到王老师选择周二、周三这两天的情况数,由概率公式计算即可;(2)用画树状图法,分别列出所有等可能出现的结果数,以及所求事件发生的结果数,然后用概率公式P= ![]() 计算即可.
计算即可.
【考点精析】认真审题,首先需要了解列表法与树状图法(当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率).


 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
【题目】如图所示,在边长为2的正三角形ABC中,E、F、G分别为AB、AC、BC的中点,点P为线段EF上一个动点,连接BP、GP,则△BPG的周长的最小值是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.
(1)求斜坡CD的高度DE;
(2)求大楼AB的高度(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直角梯形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=AB=2,OC=3,过点B作BD⊥BC,交OA于点D.将∠DBC绕点B按顺时针方向旋转,角的两边分别交y轴的正半轴、x轴的正半轴于E和F.
(1)求经过A、B、C三点的抛物线的解析式;
(2)当BE经过(1)中抛物线的顶点时,求CF的长;
(3)连接EF,设△BEF与△BFC的面积之差为S,问:当CF为何值时S最小,并求出这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCO是平行四边形,点C在x轴的负半轴上,AO=2cm,AB=4cm,∠BAO=60°,将ABCO绕点A逆时针旋转60°,得到对应的ADEF,解答下列问题: 
(1)画出旋转后的ADEF(不写作法,不证明,保留作图痕迹);
(2)求ABCO旋转过程中扫过的区域的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC与△A′B′C′都是等腰三角形,且AB=AC=5,A′B′=A′C′=3,若∠B+∠B′=90°,则△ABC与△A′B′C′的面积比为 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在8×8的正方形网格中,有一个Rt△AOB,点O是直角顶点,点O、A、B分别在网格中小正方形的顶点上,请按照下面要求在所给的网格中画图.
(1)在图1中,将△AOB先向右平移3个单位,再向上平移2个单位,得到△A1O1B1 , 画出平移后的△A1O1B1;(其中点A、O、B的对应点分别为点A1 , O1 , B1) 
(2)在图2中,△AOB与△A2O2B2是关于点P对称的图形,画出△A2O2B2 , 连接BA2 , 并直接写出tan∠A2BO的值.(其中A,O,B的对应点分别为点A2 , O2 , B2) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y1=x2+mx+n的图象经过点P(﹣3,1),对称轴是经过(﹣1,0)且平行于y轴的直线.
(1)求m,n的值.
(2)如图,一次函数y2=kx+b的图象经过点P,与x轴相交于点A,与二次函数的图象相交于另一点B,点B在点P的右侧,PA:PB=1:5,求一次函数的表达式. 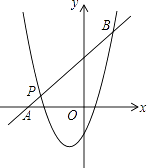
(3)直接写出y1>y2时x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com