
����Ŀ����ͼ�����κ���y=ax2+bx+c��ͼ����x��Ľ���ΪA��D��A��D���Ҳࣩ����y��Ľ���ΪC����A��4��0����C��0����3�����Գ�����ֱ��x=1��
��1������κ����Ľ���ʽ��
��2����M�ǵ���������������һ���㣬�Һ�����Ϊm�����ı���OCMA�����Ϊs����д��s��m֮��ĺ�����ϵʽ���������mΪ��ֵʱ���ı���OCMA��������
��3�����B��x���ϵĵ㣬P���������ϵĵ㣬�Ƿ���ڵ�P��ʹ����A��B��C��P�ĵ�Ϊ������ı���Ϊƽ���ı��Σ������ڣ�ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺��A��4��0�����Գ�����ֱ��x=l��
��D����2��0����
�֡�C��0����3��
�� 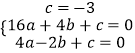
��ã�a= ![]() ��b=��
��b=�� ![]() ��c=��3��
��c=��3��
����κ�������ʽΪ��y= ![]() x2��
x2�� ![]() x��3��
x��3��
��2��
�⣺��ͼ1��ʾ��
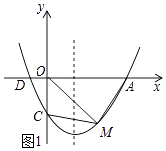
��M��m�� ![]() x2��
x2�� ![]() x��3����|yM|=��
x��3����|yM|=�� ![]() m2+
m2+ ![]() m+3��
m+3��
��S=S��ACM+S��OAM
��S= ![]() ��OC��m+
��OC��m+ ![]() ��OA��|yM|=
��OA��|yM|= ![]() ��3��m+
��3��m+ ![]() ��4������
��4������ ![]() m2+
m2+ ![]() m+3��=��
m+3��=�� ![]() m2+3m+6=��
m2+3m+6=�� ![]() ��m��2��2+9��
��m��2��2+9��
��m=2ʱ��s�����9��
��3��
�⣺��ABΪƽ���ı��εı�ʱ����AB��PC��
��PC��x�ᣮ
���P����������3��
��y=��3����ã� ![]() x2��
x2�� ![]() x��3=��3����ã�x=0��x=2��
x��3=��3����ã�x=0��x=2��
���P��������2����3����
��ABΪ�Խ���ʱ��
��ABCPΪƽ���ı��Σ�
��AB��CP����ƽ�֣�
���P��������Ϊ3��
��y=3����ã� ![]() x2��
x2�� ![]() x��3=3�������ã�x2��2x��16=0����ã�x=1+
x��3=3�������ã�x2��2x��16=0����ã�x=1+ ![]() ��x=1��
��x=1�� ![]() ��
��
�������������ڵ�P��2����3����P��1+ ![]() ��3����P��1��
��3����P��1�� ![]() ��3��ʹ����A��B��C��P�ĵ�Ϊ������ı���Ϊƽ���ı��Σ�
��3��ʹ����A��B��C��P�ĵ�Ϊ������ı���Ϊƽ���ı��Σ�
����������1�����������ߵĶԳ��Կɵõ���D���ܱ���Ȼ��A��C��D��������������ߵĽ���ʽ�����a��b��c��ֵ���Ӷ��ɵõ����κ����Ľ���ʽ����2����M��m�� ![]() x2��
x2�� ![]() x��3����|yM|=��
x��3����|yM|=�� ![]() m2+
m2+ ![]() m+3����S=S��ACM+S��OAM�ɵõ�S��m�ĺ�����ϵʽ��Ȼ�������䷽�������S�����ֵ����3����ABΪƽ���ı��εı�ʱ����AB��PC�����P��������Ϊ��3����y=��3���������ߵĽ���ʽ����õ�P�ĺ����ꣻ��ABΪ�Խ���ʱ��AB��CP����ƽ�֣����P��������Ϊ3����y=3���������ߵĽ���ʽ����õ�P�ĺ����꣮
m+3����S=S��ACM+S��OAM�ɵõ�S��m�ĺ�����ϵʽ��Ȼ�������䷽�������S�����ֵ����3����ABΪƽ���ı��εı�ʱ����AB��PC�����P��������Ϊ��3����y=��3���������ߵĽ���ʽ����õ�P�ĺ����ꣻ��ABΪ�Խ���ʱ��AB��CP����ƽ�֣����P��������Ϊ3����y=3���������ߵĽ���ʽ����õ�P�ĺ����꣮
�����㾫����������Ĺؼ�����������κ��������ʵ����֪ʶ�����������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y= ![]() x2+bx+c������B��3��0����C��0����2����ֱ��l��y=��
x2+bx+c������B��3��0����C��0����2����ֱ��l��y=�� ![]() x��
x�� ![]() ��y���ڵ�E�����������߽���A��D���㣬PΪ��������һ���㣨����A��D�غϣ���
��y���ڵ�E�����������߽���A��D���㣬PΪ��������һ���㣨����A��D�غϣ���
��1���������ߵĽ���ʽ��
��2������P��ֱ��l�·�ʱ������P��PM��x�ύl�ڵ�M��PN��y�ύl�ڵ�N����PM+PN�����ֵ��
��3����FΪֱ��l�ϵĵ㣬��E��C��P��FΪ������ı����ܷ�ƽ���ı��Σ����ܣ������F�����ꣻ�����ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ρ����Ρ������ζ���ƽ���ı��Σ������Ƕ���������������ƽ���ı��Σ������β���������ľ��Σ�Ҳ����������Σ���ˣ����ǿ����þ��Ρ����ε��������о������ε��й����⣮�ش��������⣺ 
��1����ƽ���ı��Ρ����Ρ����Ρ��������������ǵİ�����ϵ����ͼ�У�
��2��Ҫ֤��һ���ı����������Σ�����֤���ı����Ǿ��Σ���֤��������ε���ȣ�������֤���ı��������Σ���֤�����������һ������ ��
��3��ijͬѧ��������������㹫ʽ�Ƶ����Խ��߳�Ϊa�������������S=0.5a2 �� �Դ˽��ۣ�����Ϊ�Ƿ���ȷ������ȷ����˵�����ɣ�������ȷ����ٳ�һ������˵����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���ax2����a+2��x+2=0����������ȵ���������ʱ������a��ֵ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڴ�¥AB����ǰ����һб��CD��CD=4�ף��½ǡ�DCE=30�㣬С����б���µĵ�C�����¥��B������Ϊ60�㣬��б���ϵĵ�D�����¥��B������Ϊ45�㣬���е�A��C��E��ͬһֱ���ϣ�
��1����б��CD�ĸ߶�DE��
��2�����¥AB�ĸ߶ȣ�����������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪������OABC�ı�OA��y����������ϣ�OC��x����������ϣ�OA=AB=2��OC=3������B��BD��BC����OA�ڵ�D������DBC�Ƶ�B��˳ʱ�뷽����ת���ǵ����߷ֱ�y��������ᡢx�����������E��F��
��1����A��B��C����������ߵĽ���ʽ��
��2����BE������1���������ߵĶ���ʱ����CF�ij���
��3������EF�����BEF���BFC�����֮��ΪS���ʣ���CFΪ��ֵʱS��С������������Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��AB��뾶Ϊ2�ġ�O�����ڵ�C��D�ǡ�O��һ�㣬�ҡ�EDC=30�㣬��EF��AB����EF�ij���Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���糿�ܲ��������Լ��ҳ�����������2km����С��ң�����������1.5km����С��ң�Ȼ������������4.5km����ѧУ����������ܻص��Լ��ң�
��1����С����Ϊԭ�㣬����Ϊ��������1����λ���ȱ�ʾ1km����ͼ�е������ϣ��ֱ��õ�A��ʾ��С��ң��õ�B��ʾ��С��ң��õ�C��ʾ��ѧУ��λ�ã�![]()
��2����С�����ѧУ֮��ľ��룻
��3�����С���ܲ����ٶ���250m/min����ôС���ܲ�һ�����˶ʱ�䣿
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com