
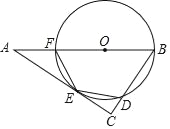
【题目】如图,点O是△ABC的边AB上一点,⊙O与边AC相切于点E,与边BC,AB分别相交于点D,F,且DE=EF.
(1)求证:∠C=90°;
(2)当BC=3,sinA=![]() 时,求AF的长.
时,求AF的长.
科目:初中数学 来源: 题型:
【题目】某商场一种商品的进价为每件30元,售价为每件40元.每天可以销售48件,为尽快减少库存,商场决定降价促销.
(1)若该商品连续两次下调相同的百分率后售价降至每件32.4元,求两次下降的百分率;
(2)经调查,若每降价0.5元,每天可多销售4件,那么每天要想获得510元的利润,每件应降价多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
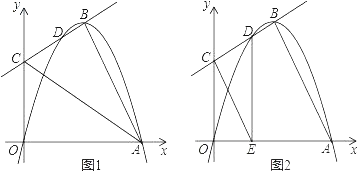
【题目】如图1,平面直角坐标系xOy中,已知抛物线y=ax2+4x与x轴交于O、A两点.直线y=kx+m经过抛物线的顶点B及另一点D(D与A不重合),交y轴于点C.
(1)当OA=4,OC=3时.
①分别求该抛物线与直线BC相应的函数表达式;
②连结AC,分别求出tan∠CAO、tan∠BAC的值,并说明∠CAO与∠BAC的大小关系;
(2)如图2,过点D作DE⊥x轴于点E,连接CE.当a为任意负数时,试探究AB与CE的位置关系?
查看答案和解析>>
科目:初中数学 来源: 题型:
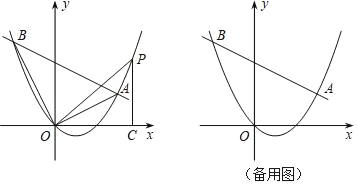
【题目】如图,在平面直角坐标系中,直线y=kx﹣4k+4与抛物线y=![]() x2﹣x交于A、B两点.
x2﹣x交于A、B两点.
(1)直线总经过定点,请直接写出该定点的坐标;
(2)点P在抛物线上,当k=﹣![]() 时,解决下列问题:
时,解决下列问题:
①在直线AB下方的抛物线上求点P,使得△PAB的面积等于20;
②连接OA,OB,OP,作PC⊥x轴于点C,若△POC和△ABO相似,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是菱形ABCD边上的一动点,它从点A出发沿着A→B→C→D路径匀速运动到点D,设△PAD的面积为y,P点的运动时间为x,则y关于x的函数图象大致为( )
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:(1)4a+2b+c<0;(2)方程ax2+bx+c=0两根都大于零;(3)y随x的增大而增大;(4)一次函数y=x+bc的图象一定不过第二象限.其中正确的个数是( )
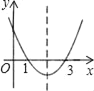
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,直径AB垂直于弦CD,垂足为E,连结AC,将△ACE沿AC翻转得到△ACF,直线FC与直线AB相交于点G.
(1)求证:FG是⊙O的切线;
(2)若B为OG的中点,CE=![]() ,求⊙O的半径长;
,求⊙O的半径长;
(3)①求证:∠CAG=∠BCG;
②若⊙O的面积为4π,GC=2![]() ,求GB的长.
,求GB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业500名员工参加安全生产知识测试,成绩记为A,B,C,D,E共5个等级,为了解本次测试的成绩(等级)情况,现从中随机抽取部分员工的成绩(等级),统计整理并制作了如下的统计图:
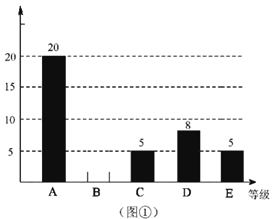
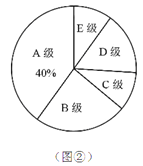
(1)求这次抽样调查的样本容量,并补全图①;
(2)如果测试成绩(等级)为A,B,C级的定为优秀,请估计该企业参加本次安全生产知识测试成绩(等级)达到优秀的员工的总人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com