
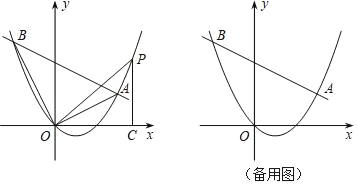
【题目】如图,在平面直角坐标系中,直线y=kx﹣4k+4与抛物线y=![]() x2﹣x交于A、B两点.
x2﹣x交于A、B两点.
(1)直线总经过定点,请直接写出该定点的坐标;
(2)点P在抛物线上,当k=﹣![]() 时,解决下列问题:
时,解决下列问题:
①在直线AB下方的抛物线上求点P,使得△PAB的面积等于20;
②连接OA,OB,OP,作PC⊥x轴于点C,若△POC和△ABO相似,请直接写出点P的坐标.
【答案】(1)![]() ;(2)①P点坐标为
;(2)①P点坐标为![]() ,
,![]() ;②
;② ![]() ,
,![]() ,
,![]() ,
,![]() .
.
【解析】
(1)直线方程化为y=k(x-4)+4,对于任意k点总有一个坐标能满足;(2)作PQ∥y轴,求出PQ,再由S△PAB等于20,根据三角形面积计算公式即可求出相应的坐标;AO=![]() ,BO=
,BO=![]() ,AB=
,AB=![]() ,再根据勾股定理和相似三角形的定义即可求出
,再根据勾股定理和相似三角形的定义即可求出![]() ,进而可求得P3和P4的值.
,进而可求得P3和P4的值.
⑴ ![]() ;
;
直线方程化为![]() ,显然,对于任意的k,点
,显然,对于任意的k,点![]() 的坐标总能满足直线方程.
的坐标总能满足直线方程.
⑵ 当![]() 时,直线方程为
时,直线方程为![]() .
.
联立方程组 解得
解得![]() ,
,![]() .
.
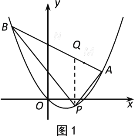
① 如图1,作![]() ∥
∥![]() 轴,交AB于点Q,则
轴,交AB于点Q,则
![]() .
.
![]()
![]() 。
。
令![]() ,即
,即![]() ,解得当
,解得当![]() 或4,相应的P点坐标为
或4,相应的P点坐标为![]() ,
,![]() ;
;
② ![]() ,
,![]() ,
,![]() ,
,![]() .
.

![]() ,
,![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() .
.
(i)△POC∽△ABO时,![]() .
.
即![]() .解得
.解得![]() ,
,![]() ,
,
得![]() ,
,![]() ;
;
(ii)△POC∽△BAO时,![]() .
.
即![]() .解得
.解得![]() ,
,![]() .
.
得![]() ,
,![]() .
.


科目:初中数学 来源: 题型:
【题目】已知直线l经过A(6,0)和B(0,12)两点,且与直线y=x交于点C,点P(m,0)在x轴上运动.
(1)求直线l的解析式;
(2)过点P作l的平行线交直线y=x于点D,当m=3时,求△PCD的面积;
(3)是否存在点P,使得△PCA成为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
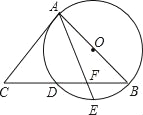
【题目】如图,AB是⊙O的直径,BC交⊙O于点D,E是![]() 的中点,AE与BC交于点F,∠C=2∠EAB.
的中点,AE与BC交于点F,∠C=2∠EAB.
(1)求证:AC是⊙O的切线;
(2)已知CD=4,CA=6,
①求CB的长;
②求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
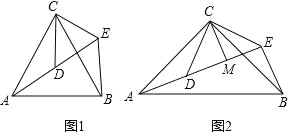
如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.填空:
①∠AEB的度数为______;
②线段AD,BE之间的数量关系为______.
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应我市创建“全国卫生城市”的号召,某校1500名学生参加了卫生知识竞赛,成绩记为A、B、C、D四等,从中随机抽取了部分学生成绩进行统计,绘制成如图两幅不完整的统计图表,根据图表信息,以下说法不正确的是( )
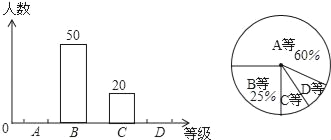
A. D等所在扇形的圆心角为15°B. 样本容量是200
C. 样本中C等所占百分比是10%D. 估计全校学生成绩为A等大约有900人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校七年级学生的英语口语水平,随机抽取该年级部分学生进行英语口语测试,学生的测试成绩按标准定为A、B、C、D四个等级,并把测试成绩绘成如图所示的两个统计图表.
七年级英语口语测试成绩统计表
成绩 | 等级 | 人数 |
| A | 12 |
| B | m |
| C | n |
| D | 9 |
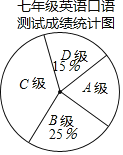
请根据所给信息,解答下列问题:
(1)本次被抽取参加英语口语测试的学生共有多少人?
(2)求扇形统计图中C级的圆心角度数;
(3)若该校七年级共有学生640人,根据抽样结课,估计英语口语达到B级以上![]() 包括B级
包括B级![]() 的学生人数.
的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
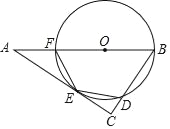
【题目】如图,点O是△ABC的边AB上一点,⊙O与边AC相切于点E,与边BC,AB分别相交于点D,F,且DE=EF.
(1)求证:∠C=90°;
(2)当BC=3,sinA=![]() 时,求AF的长.
时,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,![]() ,连结AC,过点C作直线l∥AB,点P是直线l上的一个动点,直线PA与⊙O交于另一点D,连结CD,设直线PB与直线AC交于点E.
,连结AC,过点C作直线l∥AB,点P是直线l上的一个动点,直线PA与⊙O交于另一点D,连结CD,设直线PB与直线AC交于点E.
(1)求∠BAC的度数;
(2)当点D在AB上方,且CD⊥BP时,求证:PC=AC;
(3)在点P的运动过程中
①当点A在线段PB的中垂线上或点B在线段PA的中垂线上时,求出所有满足条件的∠ACD的度数;
②设⊙O的半径为6,点E到直线l的距离为3,连结BD,DE,直接写出△BDE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:已知α、β均为锐角,tanα=![]() ,tanβ=
,tanβ=![]() ,求α+β的度数.
,求α+β的度数.
探究:(1)用6个小正方形构造如图所示的网格图(每个小正方形的边长均为1),请借助这个网格图求出α+β的度数;
延伸:(2)设经过图中M、P、H三点的圆弧与AH交于R,求![]() 的弧长.
的弧长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com