
【题目】问题:已知α、β均为锐角,tanα=![]() ,tanβ=
,tanβ=![]() ,求α+β的度数.
,求α+β的度数.
探究:(1)用6个小正方形构造如图所示的网格图(每个小正方形的边长均为1),请借助这个网格图求出α+β的度数;
延伸:(2)设经过图中M、P、H三点的圆弧与AH交于R,求![]() 的弧长.
的弧长.

 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
【题目】已知:![]() ,OB、OM、ON,是
,OB、OM、ON,是![]() 内的射线.
内的射线.
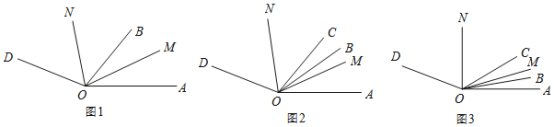
(1)如图 1,若 OM 平分 ![]() , ON平分
, ON平分![]() .当射线OB 绕点O 在
.当射线OB 绕点O 在![]() 内旋转时,
内旋转时,![]() = 度.
= 度.
(2)OC也是![]() 内的射线,如图2,若
内的射线,如图2,若![]() ,OM平分
,OM平分![]() ,ON平分
,ON平分![]() ,当射线OB绕点O在
,当射线OB绕点O在![]() 内旋转时,求
内旋转时,求![]() 的大小.
的大小.
(3)在(2)的条件下,当射线OB从边OA开始绕O点以每秒![]() 的速度逆时针旋转t秒,如图3,若
的速度逆时针旋转t秒,如图3,若![]() ,求t的值.
,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个四位自然数的百位数字大于或等于十位数字,且千位数字等于百位数字与十位数字的和,个位数字等于百位与十位数字的差,则我们称这个四位数为亲密数,例如:自然数4312,其中3>1,4=3+1,2=3-1,所以4312是亲密数;
(1)最小的亲密数是 ,最大的亲密数是 ;
(2)若把一个亲密数的千位数字与个位数字交换,得到的新数叫做这个亲密数的友谊数,请证明任意一个亲密数和它的友谊数的差都能被原亲密数的十位数字整除;
(3)若一个亲密数的后三位数字所表示的数与千位数字所表示的数的7倍之差能被13整除,请求出这个亲密数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知两种不同的数对处理器![]() 、
、![]() .当数对
.当数对![]() 输入处理器
输入处理器![]() 时,输出数对
时,输出数对![]() ,记作
,记作![]() ,
,![]() ,
,![]() ;但数对
;但数对![]() 输入处理器
输入处理器![]() 时,输出数对
时,输出数对![]() ,记作
,记作![]() ,
,![]() ,
,![]() .
.
(1)![]() ,
,![]() ( , ),
( , ),![]() ,
,![]() ( , ).
( , ).
(2)当![]() ,
,![]() ,
,![]() 时,求
时,求![]() ,
,![]() ;
;
(3)对于数对![]() ,
,![]() ,
,![]() ,
,![]() 一定成立吗?若成立,说明理由;若不成立,举例说明.
一定成立吗?若成立,说明理由;若不成立,举例说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
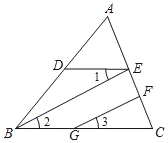
【题目】已知:如图,BE∥GF,∠1=∠3,∠DBC=70°,求∠EDB的大小.
阅读下面的解答过程,并填空(理由或数学式)
解:∵BE∥GF(已知)
∴∠2=∠3( )
∵∠1=∠3( )
∴∠1=( )( )
∴DE∥( )( )
∴∠EDB+∠DBC=180°( )
∴∠EDB=180°﹣∠DBC(等式性质)
∵∠DBC=( )(已知)
∴∠EDB=180°﹣70°=110°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应荆州市“创建全国文明城市”号召,某单位不断美化环境,拟在一块矩形空地上修建绿色植物园,其中一边靠墙,可利用的墙长不超过18m,另外三边由36m长的栅栏围成.设矩形ABCD空地中,垂直于墙的边AB=xm,面积为ym2(如图).
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)若矩形空地的面积为160m2,求x的值;
(3)若该单位用8600元购买了甲、乙、丙三种绿色植物共400棵(每种植物的单价和每棵栽种的合理用地面积如下表).问丙种植物最多可以购买多少棵?此时,这批植物可以全部栽种到这块空地上吗?请说明理由.
甲 | 乙 | 丙 | |
单价(元/棵) | 14 | 16 | 28 |
合理用地(m2/棵) | 0.4 | 1 | 0.4 |

查看答案和解析>>
科目:初中数学 来源: 题型:
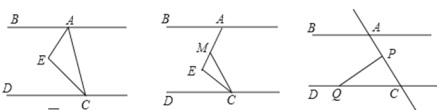
【题目】如图 ,CE 平分∠ACD,AE 平分∠BAC,∠EAC+∠ACE=90°.
(1)请判断 AB 与 CD 的位置关系,并说明理由;
(2)如图,在(1)的结论下,当∠E=90°保持不变时,移动直角顶点 E,使∠MCE=∠ECD, 当直角顶点 E 点移动时,请确定∠BAE 与![]() ∠MCD 的数量关系,并说明理由;
∠MCD 的数量关系,并说明理由;
(3)如图,在(1)的结论下,P 为线段 AC 上的一个定点,点 Q 为直线 CD 上的一个动点,当点 Q 在射线 CD 上运动时(点 C 除外)∠BAC 与∠CPQ+∠CQP 有何数量关系?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com