
【题目】计算:
(1)![]() ;
;
(2)![]() ;
;
(3)已知![]() ,求代数式
,求代数式![]() 的值.
的值.
(4)先化简,再求值:![]() ,其中a是方程
,其中a是方程 ![]() 的解.
的解.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)11;(4)
;(3)11;(4)![]() .
.
【解析】
(1)利用十字相乘法解方程即可;(2)利用平方差公式分解因式,再求解即可;(3)先求出m+n与mn的值,再代入原式求解即可;(4) 根据分式的加法和减法可以化简题目中的式子,然后求出a的值,代入化简后的式子即可求解.
解:
(1)![]() ,
,
(x+1)(3x-4)=0,
x+1=0或3x-4=0,
∴![]() ;
;
(2)![]() ,
,
(x+3)-![]() =0,
=0,
(5x-5)(-3x+11)=0,
5x-5=0或-3x+11=0,
∴![]() ;
;
(3)∵m+n=2![]() ,mn=1,
,mn=1,
∴m+mn+n=(m+n)-mn=(2![]() )-1=11;
)-1=11;
(4)![]() =
=![]()
=![]() ,
,
而![]() ,(a+3)(a-2)=0, ∴
,(a+3)(a-2)=0, ∴![]() ,
,
∵a-2≠0, ∴a=3,
∴原式=![]() =
=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】问题:已知α、β均为锐角,tanα=![]() ,tanβ=
,tanβ=![]() ,求α+β的度数.
,求α+β的度数.
探究:(1)用6个小正方形构造如图所示的网格图(每个小正方形的边长均为1),请借助这个网格图求出α+β的度数;
延伸:(2)设经过图中M、P、H三点的圆弧与AH交于R,求![]() 的弧长.
的弧长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC中,∠B=36°,∠ACB=110°,AE是∠BAC的平分线.
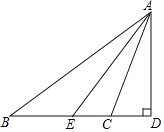
(1)求∠AEC的度数;
(2)过△ABC的顶点A作BC边上的高AD,求∠DAE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
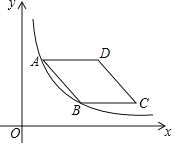
【题目】如图,菱形ABCD的边AD与x轴平行,A、B两点的横坐标分别为1和3,反比例函数y=![]() 的图象经过A、B两点,则菱形ABCD的面积是( )
的图象经过A、B两点,则菱形ABCD的面积是( )
A. 4![]() B. 4 C. 2
B. 4 C. 2![]() D. 2
D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BC是路边坡角为30°,长为10米的一道斜坡,在坡顶灯杆CD的顶端D处有一探射灯,射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是37°和60°(图中的点A、B、C、D、M、N均在同一平面内,CM∥AN).
(1)求灯杆CD的高度;
(2)求AB的长度(结果精确到0.1米).(参考数据:![]() =1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)
=1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是一垂直于水平面的建筑物,某同学从建筑物底端B出发,先沿水平方向向右行走20米到达点C,再经过一段坡度(或坡比)为i=1:0.75、坡长为10米的斜坡CD到达点D,然后再沿水平方向向右行走40米到达点E(A,B,C,D,E均在同一平面内).在E处测得建筑物顶端A的仰角为24°,则建筑物AB的高度约为(参考数据:sin24°≈0.41,cos24°≈0.91,tan24°=0.45)( )

A. 21.7米 B. 22.4米 C. 27.4米 D. 28.8米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,BC=6,CD是斜边AB上的中线,将△BCD沿直线CD翻折至△ECD的位置,连接AE.若DE∥AC,计算AE的长度等于_____.
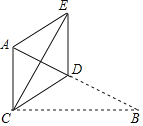
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两小朋友都从![]() 地出发,匀速步行到
地出发,匀速步行到![]() 地(
地(![]() 、
、![]() 两地之间为笔直的道路)甲出发半分钟后,乙才从
两地之间为笔直的道路)甲出发半分钟后,乙才从![]() 地出发,经过一段时间追上甲,两人继续向
地出发,经过一段时间追上甲,两人继续向![]() 地步行,当甲、乙之间的距离刚好是70米时,乙立刻掉头以原速度向
地步行,当甲、乙之间的距离刚好是70米时,乙立刻掉头以原速度向![]() 地步行,半分钟后与甲相遇,乙又立刻掉头向
地步行,半分钟后与甲相遇,乙又立刻掉头向![]() 地以原速度步行(两次掉头时间忽略不计).甲、乙相距的路程为
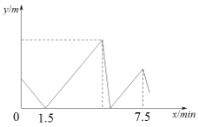
地以原速度步行(两次掉头时间忽略不计).甲、乙相距的路程为![]() (米)与乙出发的时
(米)与乙出发的时![]() (分钟)之间的关系如图所示,当乙到达
(分钟)之间的关系如图所示,当乙到达![]() 地时,甲与
地时,甲与![]() 地相距的路程是__________米.
地相距的路程是__________米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com