【题目】已知，如图，四边形ABCD中，AB=3cm，AD=4cm，BC=13cm，CD=12cm，且∠A=90°，求四边形ABCD的面积.
【答案】84
【解析】首先连接BD，再利用勾股定理计算出BD的长，再根据勾股定理逆定理计算出∠D=90°，然后计算出直角三角形ABD和直角三角形BDC的面积，即可算出答案．
解：连接BD，
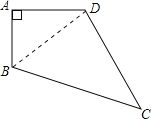
∵∠A=90°，AB=3cm，AD=4cm，
∴BD=
=
=5（cm），
∵52+122=132，
∴BD2+CD2=CB2，
∴∠BDC=90°，
∴S△DBC=
×DB×CD=
×5×12=30（cm2），
S△ABD=
×3×4=6（cm2），
∴四边形ABCD的面积为30+6=36（cm2），
故答案为：36（cm2）．
“点睛”此题主要考查了勾股定理，以及勾股定理的逆定理，解决此题的关键是算出BD的长，△BDC是直角三角形．
科目：初中数学 来源： 题型：
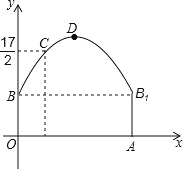
【题目】如图，隧道的截面由抛物线和长方形构成，长方形的长是12m，宽是4m．按照图中所示的直角坐标系，抛物线可以用y=﹣
x2+bx+c表示，且抛物线的点C到墙面OB的水平距离为3m时，到地面OA的距离为
m．
（1）求该抛物线的函数关系式，并计算出拱顶D到地面OA的距离；
（2）一辆货运汽车载一长方体集装箱后高为6m，宽为4m，如果隧道内设双向行车道，那么这辆货车能否安全通过？
（3）在抛物线型拱壁上需要安装两排灯，使它们离地面的高度相等，如果灯离地面的高度不超过8m，那么两排灯的水平距离最小是多少米？
查看答案和解析>>
科目：初中数学 来源： 题型：
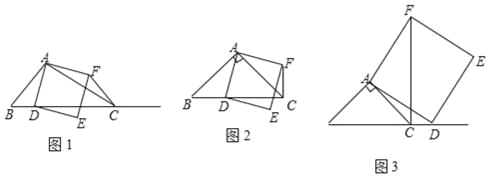
【题目】如图1，在△ABC中，∠ACB为锐角，点D为射线BC上一点，联结AD，以AD为一边且在AD的右侧作正方形ADEF．
（1）如果AB=AC，∠BAC=90°，
①当点D在线段BC上时（与点B不重合），如图2，将△ABD绕A点逆时针旋转90°，所得到的三角形为 ，线段CF、BD所在直线的位置关系为 ，线段CF、BD的数量关系为 ；
②当点D在线段BC的延长线上时，如图3，①中的结论是否仍然成立，并说明理由；
（2）如果AB≠AC，∠BAC是锐角，点D在线段BC上，当∠ACB满足什么条件时，CF⊥BC（点C、F不重合），并说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
