
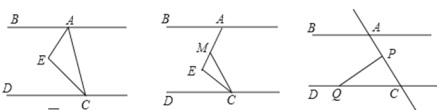
【题目】如图 ,CE 平分∠ACD,AE 平分∠BAC,∠EAC+∠ACE=90°.
(1)请判断 AB 与 CD 的位置关系,并说明理由;
(2)如图,在(1)的结论下,当∠E=90°保持不变时,移动直角顶点 E,使∠MCE=∠ECD, 当直角顶点 E 点移动时,请确定∠BAE 与![]() ∠MCD 的数量关系,并说明理由;
∠MCD 的数量关系,并说明理由;
(3)如图,在(1)的结论下,P 为线段 AC 上的一个定点,点 Q 为直线 CD 上的一个动点,当点 Q 在射线 CD 上运动时(点 C 除外)∠BAC 与∠CPQ+∠CQP 有何数量关系?为什么?
【答案】(1)AB∥CD,理由见解析;(2)∠BAE+![]() ∠MCD =90°,理由见解析;(3)∠BAC =∠CPQ+∠CQP,理由见解析
∠MCD =90°,理由见解析;(3)∠BAC =∠CPQ+∠CQP,理由见解析
【解析】
(1)根据角平分线定义得出∠ACD=2∠ACE,∠BAC=2∠EAC,求出∠ACD+∠BAC=180°,根据平行线的判定即可得出结论;
(2)作EF∥AB,易得EF∥CD∥AB,根据平行线的性质得出∠BAE=∠AEF, ∠FEC=∠ECD,再由∠AEF+∠FEC=90°,通过等量代换后即可得出结论;
(3)作PM∥AB,易得PM∥CD∥AB,根据平行线的性质得出∠BAC=∠MPC,∠MPQ=∠CQP,由∠MPC=∠MPQ+∠CPQ,通过等量代换后即可得出结论.
(1)AB∥CD,理由如下:
∵CE 平分∠ACD,AE 平分∠BAC,
∴∠ACD=2∠ACE,∠BAC=2∠EAC,
又∵∠EAC+∠ACE=90°
∴∠ACD+∠BAC=2(∠ACE+∠EAC)=180°
∴AB∥CD
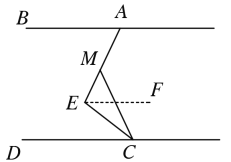
(2)∠BAE+![]() ∠MCD =90°,理由如下:
∠MCD =90°,理由如下:
如图所示,作EF∥AB,
∵AB∥CD
∴EF∥CD∥AB
∴∠BAE=∠AEF,∠FEC=∠ECD
∵∠E=90°,即∠AEF+∠FEC=90°
∴∠BAE+∠ECD=90°
又∵∠MCE=∠ECD
∴∠ECD=![]() ∠MCD
∠MCD
∴∠BAE+![]() ∠MCD =90°
∠MCD =90°
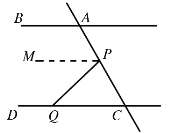
(3)∠BAC =∠CPQ+∠CQP,理由如下:
如图所示,作PM∥AB,
∵AB∥CD
∴PM∥CD∥AB
∴∠BAC=∠MPC,∠MPQ=∠CQP,
又∵∠MPC=∠MPQ+∠CPQ,
∴∠BAC=∠MPC=∠CQP+∠CPQ
即∠BAC =∠CPQ+∠CQP


科目:初中数学 来源: 题型:
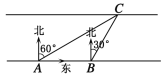
【题目】如图,甲、乙两人在道路的两边相向而行,当甲、乙两人分别行至点A、C时,测得乙在甲的北偏东60°方向上.乙留在原地休息,甲继续向前走了40米到B处,此时测得乙在其北偏东30°方向上.求道路的宽(参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
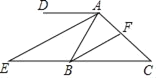
【题目】如图,AD∥EC.
(1)若∠C=40°,AB平分∠DAC,求∠DAB的度数.
(2)若AE平分∠DAB,BF平分∠ABC,试说明AE∥BF的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:已知α、β均为锐角,tanα=![]() ,tanβ=
,tanβ=![]() ,求α+β的度数.
,求α+β的度数.
探究:(1)用6个小正方形构造如图所示的网格图(每个小正方形的边长均为1),请借助这个网格图求出α+β的度数;
延伸:(2)设经过图中M、P、H三点的圆弧与AH交于R,求![]() 的弧长.
的弧长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某中学校园内有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,学校计划在中间留一块边长为(a+b)米的正方形地块修建一座雕像,然后将阴影部分进行绿化.

(1)求绿化的面积.(用含a、b的代数式表示)
(2)当a=2,b=4时,求绿化的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
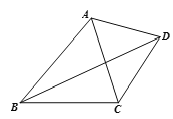
【题目】如图,已知:四边形ABCD中,对角线BD平分∠ABC,∠DCB=123°,∠ABC=50°,并且∠BAD+∠CAD=180°,那么∠DAC的度数为_________度.
查看答案和解析>>
科目:初中数学 来源: 题型:
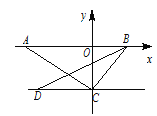
【题目】如图, A为x轴负半轴上一点, B为x轴正半轴上一点, C(0,-2),D(-3,-2).
(1)求△BCD的面积;
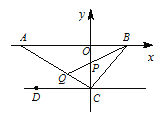
(2)若AC⊥BC,作∠CBA的平分线交CO于P,交CA于Q,判断∠CPQ与∠CQP的大小关系, 并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC中,∠B=36°,∠ACB=110°,AE是∠BAC的平分线.
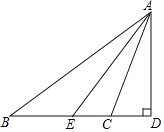
(1)求∠AEC的度数;
(2)过△ABC的顶点A作BC边上的高AD,求∠DAE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,BC=6,CD是斜边AB上的中线,将△BCD沿直线CD翻折至△ECD的位置,连接AE.若DE∥AC,计算AE的长度等于_____.
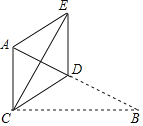
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com