
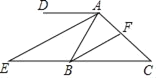
【题目】如图,AD∥EC.
(1)若∠C=40°,AB平分∠DAC,求∠DAB的度数.
(2)若AE平分∠DAB,BF平分∠ABC,试说明AE∥BF的理由.
【答案】(1)70°;(2)证明见解析
【解析】
(1)已知AD∥EC,根据两直线平行,同旁内角互补可得∠C+∠DAC=180°,即可求得∠DAC=140°,再根据角平分线的定义即可求得∠DAB=![]() ∠DAC=70°;(2)已知AD∥EC,根据两直线平行,内错角相等可得∠DAB=∠ABC;已知AE平分∠DAB,BF平分∠ABC,根据角平分线的定义可得∠EAB=
∠DAC=70°;(2)已知AD∥EC,根据两直线平行,内错角相等可得∠DAB=∠ABC;已知AE平分∠DAB,BF平分∠ABC,根据角平分线的定义可得∠EAB=![]() ∠DAB,∠ABF=
∠DAB,∠ABF=![]() ∠ABC,所以∠EAB=∠ABF,根据内错角相等,两直线平行即可判定AE∥BF.
∠ABC,所以∠EAB=∠ABF,根据内错角相等,两直线平行即可判定AE∥BF.
(1)∵AD∥EC,
∴∠C+∠DAC=180°,
∵∠C=40°,
∴∠DAC=140°,
∵AB平分∠DAC,
∴∠DAB=![]() ∠DAC=70°;
∠DAC=70°;
(2)理由是:∵AD∥EC,
∴∠DAB=∠ABC,
∵AE平分∠DAB,BF平分∠ABC,
∴∠EAB=![]() ∠DAB,∠ABF=
∠DAB,∠ABF=![]() ∠ABC,
∠ABC,
∴∠EAB=∠ABF,
∴AE∥BF.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE =∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=________度;
(2)设![]() ,
,![]() .
.
①如图2,当点在线段BC上移动,则![]() ,
,![]() 之间有怎样的数量关系?请说明理由;
之间有怎样的数量关系?请说明理由;
②当点在直线BC上移动,则![]() ,
,![]() 之间有怎样的数量关系?请直接写出你的结论.
之间有怎样的数量关系?请直接写出你的结论.




查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在求1+2+22+23+24+25+26的值时,小明发现:从第二个加数起每一个加数都是前一个加数的2倍,于是他设:S=1+2+22+23+24+25+26 为①式,然后在①式的两边都乘以2,得:2S=2+22+23+24+25+26+27 为②式;②﹣ ①得2S﹣S=27﹣1,S=27﹣1,即1+2+22+23+24+25+26=27﹣1.
(1)求1+3+32+33+34+35+36的值;
(2)求1+a+a2+a3+…+a2016(a≠0且a≠1)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个四位自然数的百位数字大于或等于十位数字,且千位数字等于百位数字与十位数字的和,个位数字等于百位与十位数字的差,则我们称这个四位数为亲密数,例如:自然数4312,其中3>1,4=3+1,2=3-1,所以4312是亲密数;
(1)最小的亲密数是 ,最大的亲密数是 ;
(2)若把一个亲密数的千位数字与个位数字交换,得到的新数叫做这个亲密数的友谊数,请证明任意一个亲密数和它的友谊数的差都能被原亲密数的十位数字整除;
(3)若一个亲密数的后三位数字所表示的数与千位数字所表示的数的7倍之差能被13整除,请求出这个亲密数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】荆州古城是闻名遐迩的历史文化名城,“五一”期间相关部门对到荆州观光游客的出行方式进行了随机抽样调查,整理后绘制了两幅统计图(尚不完整).根据图中信息,下列结论错误的是( )
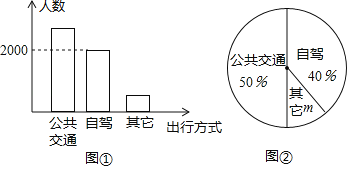
A. 本次抽样调查的样本容量是5000
B. 扇形图中的m为10%
C. 样本中选择公共交通出行的有2500人
D. 若“五一”期间到荆州观光的游客有50万人,则选择自驾方式出行的有25万人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知两种不同的数对处理器![]() 、
、![]() .当数对
.当数对![]() 输入处理器
输入处理器![]() 时,输出数对
时,输出数对![]() ,记作
,记作![]() ,
,![]() ,
,![]() ;但数对
;但数对![]() 输入处理器
输入处理器![]() 时,输出数对
时,输出数对![]() ,记作
,记作![]() ,
,![]() ,
,![]() .
.
(1)![]() ,
,![]() ( , ),
( , ),![]() ,
,![]() ( , ).
( , ).
(2)当![]() ,
,![]() ,
,![]() 时,求
时,求![]() ,
,![]() ;
;
(3)对于数对![]() ,
,![]() ,
,![]() ,
,![]() 一定成立吗?若成立,说明理由;若不成立,举例说明.
一定成立吗?若成立,说明理由;若不成立,举例说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
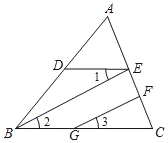
【题目】已知:如图,BE∥GF,∠1=∠3,∠DBC=70°,求∠EDB的大小.
阅读下面的解答过程,并填空(理由或数学式)
解:∵BE∥GF(已知)
∴∠2=∠3( )
∵∠1=∠3( )
∴∠1=( )( )
∴DE∥( )( )
∴∠EDB+∠DBC=180°( )
∴∠EDB=180°﹣∠DBC(等式性质)
∵∠DBC=( )(已知)
∴∠EDB=180°﹣70°=110°
查看答案和解析>>
科目:初中数学 来源: 题型:
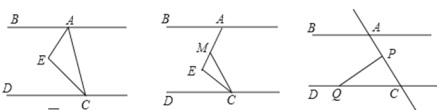
【题目】如图 ,CE 平分∠ACD,AE 平分∠BAC,∠EAC+∠ACE=90°.
(1)请判断 AB 与 CD 的位置关系,并说明理由;
(2)如图,在(1)的结论下,当∠E=90°保持不变时,移动直角顶点 E,使∠MCE=∠ECD, 当直角顶点 E 点移动时,请确定∠BAE 与![]() ∠MCD 的数量关系,并说明理由;
∠MCD 的数量关系,并说明理由;
(3)如图,在(1)的结论下,P 为线段 AC 上的一个定点,点 Q 为直线 CD 上的一个动点,当点 Q 在射线 CD 上运动时(点 C 除外)∠BAC 与∠CPQ+∠CQP 有何数量关系?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“母亲节”前夕,我市某校学生积极参与“关爱贫困母亲”的活动,他们购进一批单价为20元的“孝文化衫”在课余时间进行义卖,要求每件销售价格不得高于27元,并将所得利润捐给贫困母亲。经试验发现,若每件按22元的价格销售时,每天能卖出42件;若每件按25元的价格销售时,每天能卖出33件.假定每天销售件数y(件)与销售价格x(元/件)满足一个以x为自变量的一次函数.
(1)求y与x满足的函数关系式(不要求写出x的取值范围);
(2)在不积压且不考虑其他因素的情况下,销售价格定为多少元时,才能使每天获得的利润![]() 最大,最大利润是多少?
最大,最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com