练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

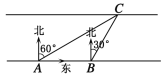
    【题目】如图，甲、乙两人在道路的两边相向而行，当甲、乙两人分别行至点A、C时，测得乙在甲的北偏东60°方向上．乙留在原地休息，甲继续向前走了40米到B处，此时测得乙在其北偏东30°方向上．求道路的宽（参考数据：）

    【答案】道路的宽约为34.64米.

    【解析】

    过C作AB的垂线，设垂足为D．易知∠BAC=30°，∠PBD=60°．∠BCA=∠BAC=30°，得CB=AB=40米；在Rt△BCD中，可用正弦函数求出DC的长．

    过点C作CD⊥AB于点D，则CD的长即为道路的宽.

    由题意得∠CAD=30°，∠CBD=60°.

    ∵∠CBD是△ACB的一个外角，

    ∴∠ACB=∠CBD-∠CAB=30°．

    ∴∠CAB=∠ACB，

    故AB=PB=40(m)．

    在Rt△BCD中，∠BDC=90°，∠CBD=60°，CB=40m，

    ∴CD=CBsin60°=40×=20≈34.64(米)．

    ∴道路的宽约为34.64米.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】阅读下列材料，并回答问题：

    如果两个两位数的十位数字相同，个位数字相加为10，那么能立即说出这两个两位数的乘积，如果这两个两位数分别写作和（即十位数字为，个位数字分别为、，，），那么它们的乘积是一个4位数，前两位数字是和的乘积，后两位数字就是和的乘积，如：，．

    （1）________；

    （2）设这两个两位数的十位数字为，个位数字分别为和，，通过计算验证这两个两位数的乘积为．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC中，AB=AC，点D是直线BC上一点（不与B、C重合），以AD为一边在AD的右侧作△ADE，使AD=AE，∠DAE =∠BAC，连接CE．

    （1）如图1，当点D在线段BC上，如果∠BAC=90°，则∠BCE=________度；

    （2）设，．

    ①如图2，当点在线段BC上移动，则，之间有怎样的数量关系？请说明理由；

    ②当点在直线BC上移动，则，之间有怎样的数量关系？请直接写出你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：，OB、OM、ON，是 内的射线．

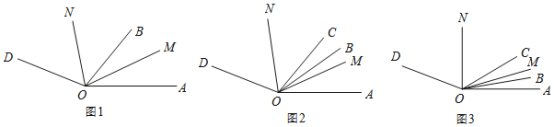
    （1）如图 1，若 OM 平分 ， ON平分．当射线OB 绕点O 在 内旋转时，= 度．

    （2）OC也是内的射线，如图2，若 ，OM平分，ON平分，当射线OB绕点O在内旋转时，求的大小．

    （3）在（2）的条件下，当射线OB从边OA开始绕O点以每秒的速度逆时针旋转t秒，如图3，若，求t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】1.概念学习.已知，点为其内部一点，连接、、，在、、中，如果存在一个三角形，其内角与的三个内角分别相等，那么就称点为的等角点.

    2.理解应用

    (1)判断以下两个命题是否为真今题，若为真令题，则在相应横线内写“真命题”；反之，则写“假命题”.

    ①内角分别为、、的三角形存在等角点； ；

    ②任意的三角形都存在等角点; ；

    （2）如图①，点是锐角的等角点，若，探究图①中，、、之间的数量关系，并说明理由.

    3.解决问题

    如图②，在中，，若的三个内角的角平分线的交点是该三角形的等角点，求三角形三个内角的度数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在求1+2+22+23+24+25+26的值时，小明发现：从第二个加数起每一个加数都是前一个加数的2倍，于是他设：S=1+2+22+23+24+25+26 为①式，然后在①式的两边都乘以2，得：2S=2+22+23+24+25+26+27 为②式；②﹣ ①得2S﹣S=27﹣1，S=27﹣1，即1+2+22+23+24+25+26=27﹣1．

    （1）求1+3+32+33+34+35+36的值；

    （2）求1+a+a2+a3+…+a2016（a≠0且a≠1）的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果一个四位自然数的百位数字大于或等于十位数字，且千位数字等于百位数字与十位数字的和，个位数字等于百位与十位数字的差，则我们称这个四位数为亲密数，例如：自然数4312，其中3＞1，4=3+1，2=3-1，所以4312是亲密数；
    （1）最小的亲密数是 ，最大的亲密数是 ；
    （2）若把一个亲密数的千位数字与个位数字交换，得到的新数叫做这个亲密数的友谊数，请证明任意一个亲密数和它的友谊数的差都能被原亲密数的十位数字整除；
    （3）若一个亲密数的后三位数字所表示的数与千位数字所表示的数的7倍之差能被13整除，请求出这个亲密数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

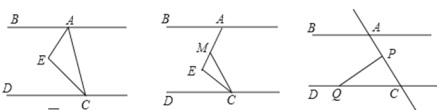
    【题目】如图 ，CE 平分∠ACD，AE 平分∠BAC，∠EAC+∠ACE＝90°．

    （1）请判断 AB 与 CD 的位置关系，并说明理由；

    （2）如图，在（1）的结论下，当∠E＝90°保持不变时，移动直角顶点 E，使∠MCE＝∠ECD， 当直角顶点 E 点移动时，请确定∠BAE 与∠MCD 的数量关系，并说明理由；

    （3）如图，在（1）的结论下，P 为线段 AC 上的一个定点，点 Q 为直线 CD 上的一个动点，当点 Q 在射线 CD 上运动时（点 C 除外）∠BAC 与∠CPQ+∠CQP 有何数量关系？为什么？

    查看答案和解析>>

    同步练习册答案