
【题目】已知直线l经过A(6,0)和B(0,12)两点,且与直线y=x交于点C,点P(m,0)在x轴上运动.
(1)求直线l的解析式;
(2)过点P作l的平行线交直线y=x于点D,当m=3时,求△PCD的面积;
(3)是否存在点P,使得△PCA成为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
【答案】(1)y=﹣2x+12;(2)S△PCD=3;(3)存在,P点坐标为(1,0)或(6+2![]() ,0)或(6﹣2
,0)或(6﹣2![]() ,0)或(2,0).
,0)或(2,0).
【解析】
(1)由A、B两点的坐标,利用待定系数法即可求得直线l的解析式;
(2)联立直线l和直线y=x,可求得C点坐标,由条件可求得直线PD的解析式,同理可求得D点坐标,则可分别求得△POD和△POC的面积,则可求得△PCD的面积;
(3)由P、A、C的坐标,可分别表示出PA、PC和AC的长,由等腰三角形的性质可得到关于m的方程,则可求得m的值,则可求得P的坐标.
解:(1)设直线l解析式为y=kx+b,
把A、B两点坐标代入可得![]() ,解得
,解得![]() ,
,
∴直线l解析式为y=﹣2x+12;
(2)解方程组![]() ,可得
,可得![]() ,
,
∴C点坐标为(4,4),
设PD解析式为y=﹣2x+n,把P(3,0)代入可得0=﹣6+n,解得n=6,
∴直线PD解析式为y=﹣2x+6,
解方程组![]() ,可得
,可得![]() ,
,
∴D点坐标为(2,2),
∴S△POD=![]() ×3×2=3,S△POC=
×3×2=3,S△POC=![]() ×3×4=6,
×3×4=6,
∴S△PCD=S△POC﹣S△POD=6﹣3=3;
(3)∵A(6,0),C(4,4),P(m,0),
∴PA2=(m﹣6)2=m2﹣12m+36,
PC2=(m﹣4)2+42=m2﹣8m+32,
AC2=(6﹣4)2+42=20,
当△PAC为等腰三角形时,则有PA=PC、PA=AC或PC=AC三种情况,
①当PA=PC时,则PA2=PC2,即m2﹣12m+36=m2﹣8m+32,
解得m=1,此时P点坐标为(1,0);
②当PA=AC时,则PA2=AC2,即m2﹣12m+36=20,
解得m=6+2![]() 或m=6﹣2
或m=6﹣2![]() ,此时P点坐标为(6+2
,此时P点坐标为(6+2![]() ,0)或(6﹣2
,0)或(6﹣2![]() ,0);
,0);
③当PC=AC时,则PC2=AC2,即m2﹣8m+32=20,解得m=2或m=6,当m=6时,P与A重合,舍去,此时P点坐标为(2,0);
综上可知存在满足条件的点P,其坐标为(1,0)或(6+2![]() ,0)或(6﹣2
,0)或(6﹣2![]() ,0)或(2,0).
,0)或(2,0).


科目:初中数学 来源: 题型:
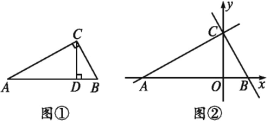
【题目】如图,在△ABC中,∠ACB=90°,CD⊥AB,
(1)图①中共有 对相似三角形,写出来分别为 (不需证明);
(2)已知AB=10,AC=8,请你求出CD的长;
(3)在(2)的情况下,如果以AB为x轴,CD为y轴,点D为坐标原点O,建立直角坐标系(如图②),若点P从点C出发,以每秒1个单位的速度沿线段CB运动,点Q从点B出发,以每秒1个单位的速度沿线段BA运动,其中一点最先到达线段的端点时,两点即刻同时停止运动;设运动时间为t秒,是否存在点P,使以点B,P,Q为顶点的三角形与△ABC相似?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
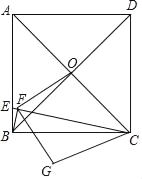
【题目】如图,正方形ABCD中,AD=4,E在AB上且AB=4BE,连接CE,作BF⊥CE于F,正方形对角线交于O点,连接OF,将△COF沿CE翻折得△CGF,连接BG,则BG的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市部分学生参加了全国初中数学竞赛决赛,并取得优异成绩.已知竞赛成绩分数都是整数,试题满分为140分,参赛学生的成绩分数分布情况如下:
分数段 | 0-19 | 20-39 | 40-59 | 60-79 | 80-99 | 100-119 | 120-140 |
人数 | 0 | 37 | 68 | 95 | 56 | 32 | 12 |
请根据以上信息解答下列问题:
(1)全市共有多少人参加本次数学竞赛决赛?最低分和最高分在什么分数范围?
(2)经竞赛组委会评定,竞赛成绩在60分以上(含60分)的考生均可获得不同等级的奖励,求我市参加本次竞赛决赛考生的获奖比例;
(3)决赛成绩分数的中位数落在哪个分数段内?
(4)上表还提供了其他信息,例如:“没获奖的人数为105人”等等.请你再写出两条此表提供的信息.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,AC为对角线,延长CD至点E使CE=CA,连接AE。F为AB上一点,且BF=DE,连接FC.
(1)若DE=1,CF=2![]() ,求CD的长。
,求CD的长。
(2)如图2,点G为线段AE的中点,连接BG交AC于H,若∠BHC+∠ABG=600,求证:AF+CE=![]() AC.
AC.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 与x轴交于A,B两点
与x轴交于A,B两点![]() 点A在点B左侧
点A在点B左侧![]() ,与y轴交于点
,与y轴交于点![]() .
.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 在抛物线的对称轴上有一点P,使
在抛物线的对称轴上有一点P,使![]() 的值最小,求点P的坐标;
的值最小,求点P的坐标;
![]() 将抛物线在B,C之间的部分记为图象
将抛物线在B,C之间的部分记为图象![]() 包含B,C两点
包含B,C两点![]() ,若直线
,若直线![]() 与图象G有公共点,请直接写出b的取值范围.
与图象G有公共点,请直接写出b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C是以AB为直径的⊙O上一动点,过点C作⊙O直径CD,过点B作BE⊥CD于点E.已知AB=6cm,设弦AC的长为xcm,B,E两点间的距离为ycm(当点C与点A或点B重合时,y的值为0).
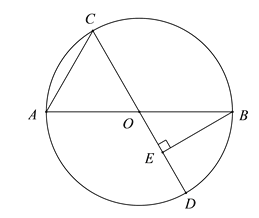
小冬根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小冬的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
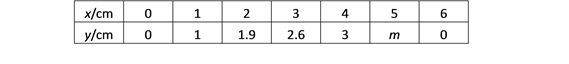
经测量m的值是(保留一位小数).
(2)建立平面直角坐标系,描出表格中所有各对对应值为坐标的点,画出该函数的图象;

(3)在(2)的条件下,当函数图象与直线![]() 相交时(原点除外),∠BAC的度数是_____.
相交时(原点除外),∠BAC的度数是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将两块斜边长相等的等腰直角三角板按如图①摆放,斜边AB分别交CD,CE于M,N点.
(1)如果把图①中的△BCN绕点C逆时针旋转90°得到△ACF,连接FM,如图②,求证:△CMF≌△CMN;
(2)将△CED绕点C旋转,则:
①当点M,N在AB上(不与点A,B重合)时,线段AM,MN,NB之间有一个不变的关系式,请你写出这个关系式,并说明理由;
②当点M在AB上,点N在AB的延长线上(如图③)时,①中的关系式是否仍然成立?

查看答案和解析>>
科目:初中数学 来源: 题型:
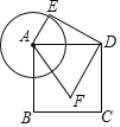
【题目】如图,已知正方形ABCD的边长为3,以点A为圆心,1为半径作圆,E是⊙A上的任意一点,将DE绕点D按逆时针旋转90°,得到DF,连接AF,
(1)当∠EAD=90°时,AF=________________.
(2)在E的整个运动过程中,AF的最大值是________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com