
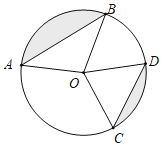
【题目】如图,已知⊙O的半径为5,弦AB=8,CD=6,则图中阴影部分面积为( )
A. ![]() π–24 B. 9π C.
π–24 B. 9π C. ![]() π–12 D. 9π–6
π–12 D. 9π–6
【答案】A
【解析】
过点O作OE⊥AB于E,作OF⊥CD于F,根据垂径定理求出AE、CF,再利用勾股定理列式求出OE=OF,从而得到AE=OF,OE=CF,然后利用“边角边”证明△AOE和△OCF全等,根据全等三角形对应角相等可得∠AOE=∠OCF,再求出∠AOE+∠COF=90°,然后求出∠AOB+∠COD=180°,把弧CD旋转到点D与点B重合,构建直角三角形ABC;然后根据圆的面积公式和直角三角形的面积公式来求阴影部分的面积:阴影面积=半圆面积-直角三角形ABC的面积.
解:如图1,过点O作OE⊥AB于E,作OF⊥CD于F,

由垂径定理得,AE=![]() AB=
AB=![]() ×8=4,CF=
×8=4,CF=![]() CD=
CD=![]() ×6=3,
×6=3,
由勾股定理得,OE=![]() =
=![]() =3,
=3,
OF=![]() =
=![]() =4,
=4,
∴AE=OF,OE=CF,
在△AOE和△OCF中,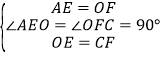 ,
,
∴△AOE≌△OCF(SAS),∴∠AOE=∠OCF,
∵∠OCF+∠COF=90°,∴∠AOE+∠COF=90°,
∴∠AOB+∠COD=2(∠AOE+∠COF)=2×90°=180°,
如图2把弧CD旋转到点D与点B重合.
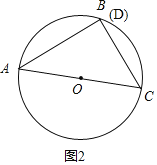
∴△ABC为直角三角形,且AC为圆的直径;
∵AB=8,CD=6,∴AC=10(勾股定理),
∴阴影部分的面积=S半圆–S△ABC=![]() π×52–
π×52–![]() ×6×8=
×6×8=![]() π–24;
π–24;
故选A.


科目:初中数学 来源: 题型:
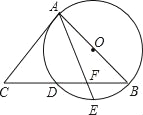
【题目】如图,AB是⊙O的直径,BC交⊙O于点D,E是![]() 的中点,AE与BC交于点F,∠C=2∠EAB.
的中点,AE与BC交于点F,∠C=2∠EAB.
(1)求证:AC是⊙O的切线;
(2)已知CD=4,CA=6,
①求CB的长;
②求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
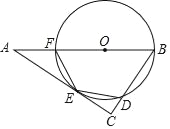
【题目】如图,点O是△ABC的边AB上一点,⊙O与边AC相切于点E,与边BC,AB分别相交于点D,F,且DE=EF.
(1)求证:∠C=90°;
(2)当BC=3,sinA=![]() 时,求AF的长.
时,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,![]() ,连结AC,过点C作直线l∥AB,点P是直线l上的一个动点,直线PA与⊙O交于另一点D,连结CD,设直线PB与直线AC交于点E.
,连结AC,过点C作直线l∥AB,点P是直线l上的一个动点,直线PA与⊙O交于另一点D,连结CD,设直线PB与直线AC交于点E.
(1)求∠BAC的度数;
(2)当点D在AB上方,且CD⊥BP时,求证:PC=AC;
(3)在点P的运动过程中
①当点A在线段PB的中垂线上或点B在线段PA的中垂线上时,求出所有满足条件的∠ACD的度数;
②设⊙O的半径为6,点E到直线l的距离为3,连结BD,DE,直接写出△BDE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在□ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.
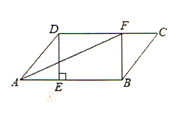
(1)求证:四边形BFDE是矩形;
(2)若AF平分∠BAD,且AE=3,DE=4,求矩形BFDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=8cm,AC=6cm,动点P从点C出发沿CB方向以3cm/s的速度向点B运动,同时动点Q从点B出发沿BA方向以2cm/s的速度向点A运动,将△APQ沿直线AB翻折得△AP′Q,若四边形APQP′为菱形,则运动时间为( )

A. 1sB. ![]()
![]() sC.
sC. ![]() sD.
sD. ![]() s
s
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程(x-2)(x-3)=m有实数根x1,x2,且x1≠x2,有下列结论:
①x1=2,x2=3; ②![]() ;
;
③二次函数y=(x-x1)(x-x2)+m的图象与x轴交点的坐标为(2,0)和(3,0).
其中,正确结论的个数是( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:已知α、β均为锐角,tanα=![]() ,tanβ=
,tanβ=![]() ,求α+β的度数.
,求α+β的度数.
探究:(1)用6个小正方形构造如图所示的网格图(每个小正方形的边长均为1),请借助这个网格图求出α+β的度数;
延伸:(2)设经过图中M、P、H三点的圆弧与AH交于R,求![]() 的弧长.
的弧长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件50元.当售价为每件70元时,每星期可卖出300件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.在确保盈利的前提下,解答下列问题:
(1)若设每件降价x元、每星期售出商品的利润为y元,请写出y与x的函数关系式,并求出自变量x的取值范围;
(2)当降价多少元时,每星期的利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com