
【题目】今年某市为创评“全国文明城市”称号,周末团市委组织志愿者进行宣传活动.班主任梁老师决定从4名女班干部(小悦、小惠、小艳和小倩)中通过抽签方式确定2名女生去参加.抽签规则:将4名女班干部姓名分别写在4张完全相同的卡片正面,把四张卡片背面朝上,洗匀后放在桌面上,梁老师先从中随机抽取一张卡片,记下姓名,再从剩余的3张卡片中随机抽取第二张,记下姓名.
(1)该班男生“小刚被抽中”是 事件,“小悦被抽中”是 事件(填“不可能”或“必然”或“随机”);第一次抽取卡片“小悦被抽中”的概率为 ;
(2)试用画树状图或列表的方法表示这次抽签所有可能的结果,并求出“小惠被抽中”的概率.
【答案】(1)不可能、随机、![]() ;(2)
;(2)![]() .
.
【解析】
(1)4张完全相同的卡片正面写的都是女班干部,所以不可能抽到男生;
“小悦被抽中”可能发生,也可能不发生,所以是随机事件;
第一次抽取卡片,4名女生都有可能被抽到,结果有4种,并且被抽到的概率都相等,所以“小悦被抽中”的概率为![]() ;
;
(2)利用树状图或者列表法将所有可能的结果全部列出来,12种,从中找出满足“小惠被抽中”的情况有6种,等可能情况下,随机事件的概率![]() 所求情况数与总情况数之比,代入计算即可.
所求情况数与总情况数之比,代入计算即可.
解:(1)该班男生“小刚被抽中”是不可能事件,“小悦被抽中”是随机事件,第一次抽取卡片“小悦被抽中”的概率为![]() ,
,
故答案为:不可能、随机、![]() ;
;
(2)记小悦、小惠、小艳和小倩这四位女同学分别为A、B、C、D,
列表如下:
A | B | C | D | |
A | ﹣﹣﹣ | (B,A) | (C,A) | (D,A) |
B | (A,B) | ﹣﹣﹣ | (C,B) | (D,B) |
C | (A,C) | (B,C) | ﹣﹣﹣ | (D,C) |
D | (A,D) | (B,D) | (C,D) | ﹣﹣﹣ |
由表可知,共有12种等可能结果,其中小惠被抽中的有6种结果,
所以小惠被抽中的概率为![]() =
=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
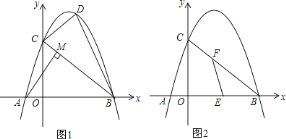
【题目】如图![]() ,在平面直角坐标系中,直线
,在平面直角坐标系中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,点
,点![]() 为
为![]() 轴负半轴上一点,
轴负半轴上一点,![]() 于点
于点![]() 交
交![]() 轴于点
轴于点![]() ,满足
,满足![]() .已知抛物线
.已知抛物线![]() 经过点
经过点![]() 、
、![]() 、
、![]() .
.
![]() 求抛物线的函数关系式;
求抛物线的函数关系式;
![]() 连接
连接![]() ,点
,点![]() 在线段
在线段![]() 上方的抛物线上,连接
上方的抛物线上,连接![]() 、
、![]() ,若
,若![]() 和
和![]() 面积满足
面积满足![]() ,求点
,求点![]() 的坐标;
的坐标;
![]() 如图
如图![]() ,
,![]() 为
为![]() 中点,设
中点,设![]() 为线段
为线段![]() 上一点(不含端点),连接
上一点(不含端点),连接![]() .一动点
.一动点![]() 从
从![]() 出发,沿线段
出发,沿线段![]() 以每秒
以每秒![]() 个单位的速度运动到
个单位的速度运动到![]() ,再沿着线段
,再沿着线段![]() 以每秒
以每秒![]() 个单位的速度运动到
个单位的速度运动到![]() 后停止.若点
后停止.若点![]() 在整个运动过程中用时最少,请直接写出最少时间和此时点
在整个运动过程中用时最少,请直接写出最少时间和此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有![]() 、
、![]() 、
、![]() 三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )
三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )

A.在∠A、∠B两内角平分线的交点处
B.在AC、BC两边垂直平分线的交点处
C.在AC、BC两边高线的交点处
D.在AC、BC两边中线的交点处
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲和乙一起做游戏,下列游戏规则对双方公平的是( )

A. 在一个装有2个红球和3个白球(每个球除颜色外都相同)的袋中任意摸出一球,摸到红球甲获胜,摸到白球乙获胜;
B. 从标有号数1到100的100张卡片中,随意抽取一张,抽到号数为奇数甲获胜,否则乙获胜;
C. 任意掷一枚质地均匀的骰子,掷出的点数小于4则甲获胜,掷出的点数大于4则乙获胜;
D. 让小球在如图所示的地板上自由地滚动,并随机地停在某块方块上,若小球停在黑色区域则甲获胜,若停在白色区域则乙获胜
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙三个盒子中分别装有除颜色外都相同的小球,甲盒中装有两个球,分别为一个红球和一个绿球;乙盒中装有三个球,分别为两个绿球和一个红球;丙盒中装有两个球,分别为一个红球和一个绿球,从三个盒子中各随机取出一个小球
(1)请画树状图,列举所有可能出现的结果
(2)请直接写出事件“取出至少一个红球”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某蔬菜生产基地用装有恒温系统的大棚栽培一种适宜生长温度为15﹣20℃的新品种,如图是某天恒温系统从开启到关闭及关闭后,大棚里温度y(℃)随时间x(h)变化的函数图象,其中AB段是恒温阶段,BC段是双曲线![]() 的一部分,请根据图中信息解答下列问题:
的一部分,请根据图中信息解答下列问题:
(1)求k的值;
(2)恒温系统在一天内保持大棚里温度在15℃及15℃以上的时间有多少小时?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=2x﹣2与x轴交于点A,与y轴交于点B.
(1)求点A,B的坐标;
(2)画出直线AB,并求△OAB的面积;
(3)点C在x轴上,且AC=AB,直接写出点C坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
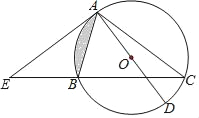
【题目】如图,△ABC内接于⊙O,AD是⊙O直径,E是CB延长线上一点,且∠BAE=∠C.
(1)求证:直线AE是⊙O的切线;
(2)若∠BAE=30°,⊙O的半径为2,求阴影部分的面积;
(3)若EB=AB,cos∠E=![]() ,AE=24,求EB的长及⊙O的半径.
,AE=24,求EB的长及⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com