
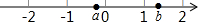
分析 (1)由数轴确定a,b的取值范围,根据绝对值的性质化简即可;
(2)①根据数轴上两点间的距离=两个数之差的绝对值,算出即可;
②表示出AB的距离,根据绝对值等于2的数有2或-2两个,解答出即可;
③|x+1|+|x-2|的最小值,意思是x到-1的距离与到2的距离之和最小,那么x应在-1和2之间的线段上.
解答 解:由数轴可得:-1<a<0,1<b<2,
(1)|2-(-a+1)|-|b-2|+|a-b|
=|2+a-1|+(b-2)-(a-b)
=1+a+b-2-a+b
=2b-1.
(2)①数轴上表示1和4的两点之间的距离是:4-1=3,故答案为3;
②数轴上x和-2的两点A和B之间的距离是|x-(-2)|=|x+2|,
如果两点A和B之间的距离是2,
则|x+2|=2,
解得:x=0或x=-4,
故答案为:|x+2|,0或-4;
③在数轴上|x+1|+|x-2|的几何意义是:表示有理数x的点到-1及到3的距离之和,所以当-1≤x≤2时,它的最小值为3,
故答案为:3,-1≤x≤2.
点评 本题主要考查了数轴和绝对值,掌握数轴上两点间的距离=两个数之差的绝对值,绝对值是正数的数有2个.


科目:初中数学 来源: 题型:填空题
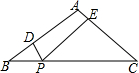 在△ABC中,AB=AC=5,BC=8,点P是BC上的动点,过点P作PD⊥AB于点D,PE⊥AC于E,则PD+PE=$\frac{24}{5}$.
在△ABC中,AB=AC=5,BC=8,点P是BC上的动点,过点P作PD⊥AB于点D,PE⊥AC于E,则PD+PE=$\frac{24}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
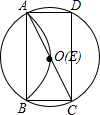 已知⊙O为矩形ABCD的外接圆,⊙O的半径为r,将劣弧沿弦AB翻折交AC于点E,连接BE.
已知⊙O为矩形ABCD的外接圆,⊙O的半径为r,将劣弧沿弦AB翻折交AC于点E,连接BE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com