
【题目】如图,BD、CE是△ABC的高,BD和CE相交于点O。
(1)图中有哪几个直角三角形?
(2)图中有与∠2相等的角吗?请说明理由。
(3)若∠4=55°,∠ACB=65°,求∠3,∠5的度数。
【答案】
(1)解:直角三角形有:△BOE、△BCE、△ACE、△BCD、△COD、△ABD
(2)解:与∠2相等的角是∠1.理由如下:∵BD、CE是△ABC的高,
∴∠1+∠A=90°,∠2+∠A=90°,
∴∠1=∠2,
∴与∠2相等的角是∠1
(3)解:∵∠ACB=65°,BD是高,∴∠3=90°-∠ACB=90°-65°=25°,
在△BOC中,∠BOC=180°-∠3-∠4=180°-25°-55°=100°,
∴∠5=∠BOC=100°
【解析】(1)利用直角三角形定义和高的意义,可得出6个直角三角形;(2)利用”同角(等角)的余角相等“,可推出∠1=∠2;(3)利用内角和定理,可求出答案.


科目:初中数学 来源: 题型:
【题目】如图所示,∠E=∠F,∠B=∠C,AE=AF,以下结论:①∠FAN=∠EAM;②EM=FN;③△ACN≌△ABM;④CD=DN.其中正确的有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
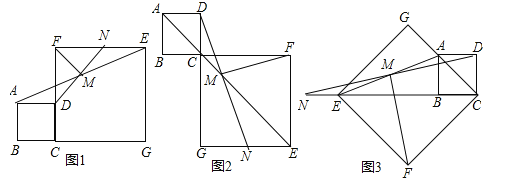
【题目】如图1所示,在正方形ABCD和正方形CGEF中,点B、C、G在同一条直线上,M是线段AE的中点,DM的延长线交EF于点N,连接FM,易证:DM=FM,DM⊥FM(无需写证明过程)
(1)如图2,当点B、C、F在同一条直线上,DM的延长线交EG于点N,其余条件不变,试探究线段DM与FM有怎样的关系?请写出猜想,并给予证明;
(2)如图3,当点E、B、C在同一条直线上,DM的延长线交CE的延长线于点N,其余条件不变,探究线段DM与FM有怎样的关系?请直接写出猜想.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com