
����Ŀ����ͼ1��ʾ����������ABCD��������CGEF�У���B��C��G��ͬһ��ֱ���ϣ�M���߶�AE���е㣬DM���ӳ��߽�EF�ڵ�N������FM����֤��DM=FM��DM��FM������д֤�����̣�
��1����ͼ2������B��C��F��ͬһ��ֱ���ϣ�DM���ӳ��߽�EG�ڵ�N�������������䣬��̽���߶�DM��FM�������Ĺ�ϵ����д�����룬������֤����
��2����ͼ3������E��B��C��ͬһ��ֱ���ϣ�DM���ӳ��߽�CE���ӳ����ڵ�N�������������䣬̽���߶�DM��FM�������Ĺ�ϵ����ֱ��д�����룮
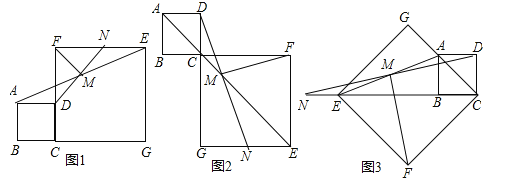
���𰸡���1��DM=FM��DM��FM��֤���������������2��DM=FM��DM��FM��
��������
�����������1������DF��NF�������������������õ�AD��BC��BC��GE��������AD��GE���õ���DAM=��NEM������֤����MAD�ա�MEN���ó�DM=MN��AD=EN���Ƴ���MAD�ա�MEN����DFN�ǵ���ֱ�������Σ����ɵõ����ۣ�
��2������DF��NF�������������������õ�AD��BC��AD��CN�������õ���DAM=��NEM����֤��MAD�ա�MEN����DM=MN��AD=EN���Ƴ���MAD�ա�MEN����DFN�ǵ���ֱ�������Σ��������õ����ۣ�
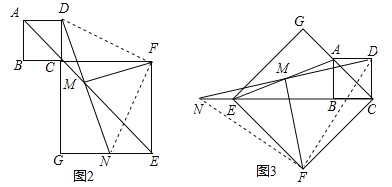
�����������1����ͼ2��DM=FM��DM��FM��֤�����£�
����DF��NF�����ı���ABCD��CGEF�������Σ���AD��BC��BC��GE����AD��GE�����DAM=��NEM����M��AE���е㣬��AM=EM������MAD����MEN�У��ߡ�AMD=��EMN��AM=EM����DAM=��NEM�����MAD�ա�MEN����DM=MN��AD=EN����AD=CD����CD=NE����CF=EF����DCF=��DCB=90�㣬����DCF����NEF�У���CD=EN����DCF=��NEF=90����CF=EF�����MAD�ա�MEN����DF=NF����CFD=��EFN���ߡ�EFN+��NFC=90�㣬���DFC+��CFN=90�㣬���DFN=90�㣬��DM��FM��DM=FM��
��2�����룺DM��FM��DM=FM��
֤�����£���ͼ3������DF��NF�����ı���ABCD�������Σ���AD��BC������E��B��C��ͬһ��ֱ���ϣ���AD��CN�����ADN=��MNE������MAD����MEN�У��ߡ�AMD=��EMN��AM=EM����DAM=��NEM�����MAD�ա�MEN����DM=MN��AD=EN����AD=CD����CD=NE����CF=EF���ߡ�DCF=90��+45��=135�㣬��NEF=180�㩁45��=135�㣬���DCF=��NEF������DCF����NEF�У���CD=NE����DCF=��NEF=135����CF=EF�����MAD�ա�MEN����DF=NF����CFD=��EFN���ߡ�CFD+��EFD=90�㣬���NFE+��EFD=90�㣬���DFN=90�㣬��DM��FM��DM=FM��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�߶�AB��CD�Ĺ�������BD= ![]() AB=
AB= ![]() CD �� �߶�AB��CD���е�E �� F֮�������10cm �� ��AB �� CD�ij���
CD �� �߶�AB��CD���е�E �� F֮�������10cm �� ��AB �� CD�ij���![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��ģ���Ժ���ѧ�Ƴ���ʦ��һ�����ѧ�ɼ��Ƴ���ͼ��ͳ��ͼ�������˼�����Ϣ����ǰ�����Ƶ�ʺ���0.14���ڵ�һ���Ƶ����0.02���������ҵڶ������������Ƶ����Ϊ3��9��8��Ȼ����ѧ����Ҳ����һ�𣩽��ͳ��ͼ����������⣺ 
��1��ȫ��ѧ���Ƕ����ˣ�
��2���ɼ�������90��Ϊ���㣬��ôȫ��ɼ����������Ƕ��٣�
��3����������100�ֿ��Եõ�A+�ȼ�����С���õ�A+�ĸ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ε����������߶���һ���ܽ������ηֳ������ȵ������ֵ��ǣ� ��
A.��ƽ����
B.���
C.��
D.����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��BD��CE�ǡ�ABC�ĸߣ�BD��CE�ཻ�ڵ�O��
��1��ͼ�����ļ���ֱ�������Σ�
��2��ͼ�������2��ȵĽ�����˵�����ɡ�
��3������4=55�㣬��ACB=65�㣬���3����5�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��2��3�ֱ�����ABC��AB��ACΪ������ABC�����������Σ��ȱ������Σ������ı��Σ������Σ���������Σ�BE��CD�ཻ�ڵ�O��
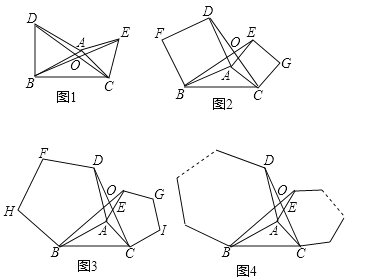
��1����ͼ1�У���֤����ABE�ա�ADC��
��2���ɣ�1��֤����ABE�ա�ADC���ɴ˿��Ƶ���ͼ1����BOC=120�㣬����̽����ͼ2�У���BOC�Ķ�������˵�����ɻ�д��֤�����̣�
��3����գ���������1����2���Ļ����Ͽɵ���ͼ3����BOC= ����д��������
��4���ɴ��ƹ㵽һ�����Σ���ͼ4�����ֱ�����ABC��AB��ACΪ������ABC������n���Σ�BE��CD���ཻ�ڵ�O���������BOC�Ķ���Ϊ ���ú�n��ʽ�ӱ�ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����x��1�ǹ���x�ķ���2x+a��6�Ľ⣬��ôa��ֵ�ǣ�������
A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ACB=90�㣬��A=20�㣬������ABC��CD�۵���ʹ��B����AC���ϵĵ�E�������CED�Ķ����ǣ� �� 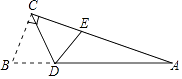
A.30��
B.40��
C.50��
D.70��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com