
����Ŀ����ͼ1��2��3�ֱ�����ABC��AB��ACΪ������ABC�����������Σ��ȱ������Σ������ı��Σ������Σ���������Σ�BE��CD�ཻ�ڵ�O��
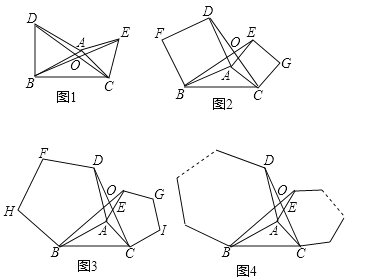
��1����ͼ1�У���֤����ABE�ա�ADC��
��2���ɣ�1��֤����ABE�ա�ADC���ɴ˿��Ƶ���ͼ1����BOC=120�㣬����̽����ͼ2�У���BOC�Ķ�������˵�����ɻ�д��֤�����̣�
��3����գ���������1����2���Ļ����Ͽɵ���ͼ3����BOC= ����д��������
��4���ɴ��ƹ㵽һ�����Σ���ͼ4�����ֱ�����ABC��AB��ACΪ������ABC������n���Σ�BE��CD���ཻ�ڵ�O���������BOC�Ķ���Ϊ ���ú�n��ʽ�ӱ�ʾ����
���𰸡���1��֤������������2����BOC=90������3��72������4��![]() ��
��
��������
�����������1�����ݵȱ�������֤��AB=AD��AC=AE�������õ�ʽ���ʵ���DAC=��BAE������SAS�ó���ABE�ա�ADC��
��2����������������֤����ABE�ա�ADC������BEA=��DCA������������ACEG���ڽ���EAC=90�����������ǺͶ�������BOC=90�㣻
��3������������ε�����֤������ADC�ա�ABM���ټ��������ÿһ���ڽǵĶ���Ϊ108�㣬����������Ƕ��������BOC=72�㣻
��4��������n���ε�����֤������ADC�ա�ABM���ټ���n����ÿһ���ڽǵĶ���Ϊ180�㩁![]() ������������Ƕ��������BOC=
������������Ƕ��������BOC=![]() ��
��
�����������1����ͼ1���ߡ�ABD����ACE�ǵȱ������Σ���AB=AD��AC=AE����DAB=��EAC=60�㣬���DAB+��BAC=��EAC+��BAC������DAC=��BAE�����ABE�ա�ADC��
��2����ͼ2����BOC=90�㣬�����ǣ�
���ı���ABFD���ı���ACGE���������Σ���AB=AD��AC=AE����DAB=��EAC=90�㣬���BAE=��DAC�����ADC�ա�ABE�����BEA=��DCA���ߡ�EAC=90�㣬���AMC+��DCA=90�㣬�ߡ�BOC=��OME+��BEA=��AMC+��DCA�����BOC=90�㣻
��3����ͼ3��ͬ���ã���ADC�ա�ABM�����BME=��DCA���ߡ�BOC=��BME+��OEM=��DCA+��AEC�����������ACIGM�����EAC=180�㩁![]() =108�㣬���DCA+��AEC=72�㣬���BOC=72�㣻
=108�㣬���DCA+��AEC=72�㣬���BOC=72�㣻
�ʴ�Ϊ��72�㣻
��4����ͼ4����BOC�Ķ���Ϊ![]() �������ǣ�
�������ǣ�
ͬ���ã���ADC�ա�ABM�����BME=��DCA���ߡ�BOC=��BME+��OEM=��DCA+��AEC������n����AC��M�����EAC=180�㩁![]() �����DCA+��AEC=180�㩁��180����
�����DCA+��AEC=180�㩁��180����![]() �������BOC=
�������BOC=![]() ��
��


 ����������������ϵ�д�
����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Rt��ABC�У���BAC=90�㣬����B��ֱ��MN��AC��DΪBC����һ�㣬����AD����DE��AD��MN�ڵ�E������AE��
��1����ͼ�٣�����ABC=45��ʱ����֤��AD=DE��
��2����ͼ�ڣ�����ABC=30��ʱ���߶�AD��DE�к�������ϵ������˵�����ɣ�
��3������ABC=��ʱ����ֱ��д���߶�AD��DE��������ϵ�����ú��������Ǻ�����ʾ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
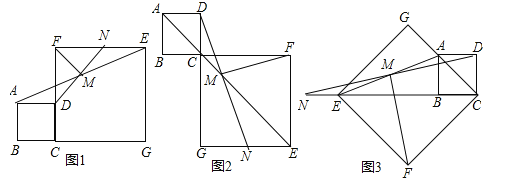
����Ŀ����ͼ1��ʾ����������ABCD��������CGEF�У���B��C��G��ͬһ��ֱ���ϣ�M���߶�AE���е㣬DM���ӳ��߽�EF�ڵ�N������FM����֤��DM=FM��DM��FM������д֤�����̣�
��1����ͼ2������B��C��F��ͬһ��ֱ���ϣ�DM���ӳ��߽�EG�ڵ�N�������������䣬��̽���߶�DM��FM�������Ĺ�ϵ����д�����룬������֤����
��2����ͼ3������E��B��C��ͬһ��ֱ���ϣ�DM���ӳ��߽�CE���ӳ����ڵ�N�������������䣬̽���߶�DM��FM�������Ĺ�ϵ����ֱ��д�����룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��ģ���Ժ���ѧ�Ƴ���ʦ��һ�����ѧ�ɼ��Ƴ���ͼ��ͳ��ͼ�������˼�����Ϣ����ǰ�����Ƶ�ʺ���0.14���ڵ�һ���Ƶ����0.02���������ҵڶ������������Ƶ����Ϊ3��9��8��Ȼ����ѧ����Ҳ����һ�𣩽��ͳ��ͼ����������⣺ 
��1��ȫ��ѧ���Ƕ����ˣ�
��2���ɼ�������90��Ϊ���㣬��ôȫ��ɼ����������Ƕ��٣�
��3����������100�ֿ��Եõ�A+�ȼ�����С���õ�A+�ĸ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�ڡ�ABC�У�CD�Ǹߣ���E��F��G�ֱ���BC��AB��AC�ϣ���EF��AB����1=��2�����ж�DG��BC��λ�ù�ϵ����˵�����ɡ�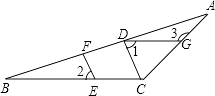
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
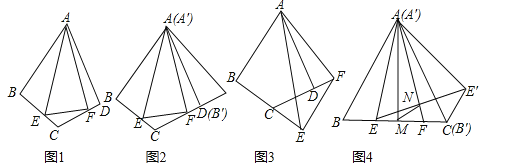
����Ŀ����ѧϰ��ͼ�ε���ת֪ʶ����ѧ��ȤС���ͬѧ���ֽ�һ����ͼ����תǰ����߶�֮�䡢��֮��Ĺ�ϵ������̽����
��һ������̽��
��ͼ1�����ı���ABCD�У�AB=AD����BAD=60�㣬��ABC=��ADC=90�㣬��E��F�ֱ����߶�BC��CD�ϣ���EAF=30�㣬����EF��
��1����ͼ2������ABE�Ƶ�A��ʱ����ת60���õ���A��B��E�䣨A��B����AD�غϣ�����ֱ��д����E��AF= �ȣ��߶�BE��EF��FD֮���������ϵΪ ��
��2����ͼ3��������E��F�ֱ����߶�BC��CD���ӳ�����ʱ�������������䣬��̽���߶�BE��EF��FD֮���������ϵ����˵�����ɣ�
��������չ����
��ͼ4���ڵȱ���ABC�У�E��F�DZ�BC�ϵ����㣬��EAF=30�㣬BE=1������ABE�Ƶ�A��ʱ����ת60��õ���A��B��E�䣨A��B����AC�غϣ�������EE�䣬AF��EE�佻�ڵ�N������A��AM��BC�ڵ�M������MN�����߶�MN�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��һ������˿Χ�ɵ���������������һ�����Ƶ�������������ͼ2��������һ���뾶Ϊr��Բ�Ľ�90�������A2OB2������A2C2EO��B2D2EO�������ɸ�ȱһ�ߵľ���״��A1C1D1B1��A2C2D2B2������AnBnCnDn��OEFGΧ�ɣ�����A1��G��B1��![]() �ϣ�A2��A3����An��B2��B3����Bn�ֱ��ڰ뾶OA2��OB2�ϣ�C2��C3������Cn��D2��D3��Dn�ֱ���EC2��ED2�ϣ�EF��C2D2��H2��C1D1��EF��H1��FH1=H1H2=d��C1D1��C2D2��C3D3��CnDn���εȾ���ƽ���ŷţ����һ������״��ı�CnDn���E��ľ���Ӧ������d����A1C1��A2C2��A3C3�Ρ���AnCn��
�ϣ�A2��A3����An��B2��B3����Bn�ֱ��ڰ뾶OA2��OB2�ϣ�C2��C3������Cn��D2��D3��Dn�ֱ���EC2��ED2�ϣ�EF��C2D2��H2��C1D1��EF��H1��FH1=H1H2=d��C1D1��C2D2��C3D3��CnDn���εȾ���ƽ���ŷţ����һ������״��ı�CnDn���E��ľ���Ӧ������d����A1C1��A2C2��A3C3�Ρ���AnCn��
��1����d��ֵ��
��2���ʣ�CnDn���E��ľ����ܷ����d������ܣ����������n��ֵ��������ܣ���ô����֮��ľ����Ƕ��٣�
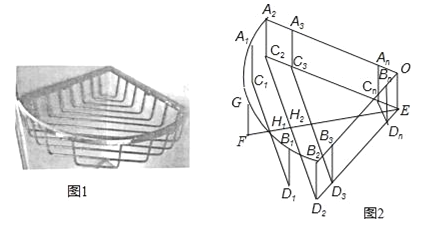
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��l���ı���ABCD�ĶԳ��ᣬAD��BC���ָ������н��ۣ� ��AB��CD����AB=BC����AB��BC����AO=OC��������ȷ�Ľ����У� ��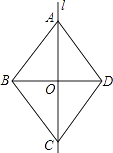
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com