
【题目】在学习了图形的旋转知识后,数学兴趣小组的同学们又进一步对图形旋转前后的线段之间、角之间的关系进行了探究.
(一)尝试探究
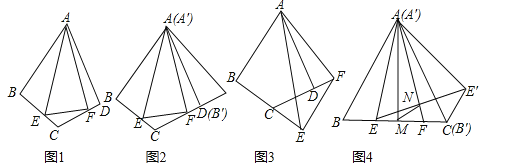
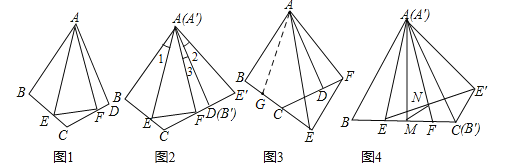
如图1,在四边形ABCD中,AB=AD,∠BAD=60°,∠ABC=∠ADC=90°,点E、F分别在线段BC、CD上,∠EAF=30°,连接EF.
(1)如图2,将△ABE绕点A逆时针旋转60°后得到△A′B′E′(A′B′与AD重合),请直接写出∠E′AF= 度,线段BE、EF、FD之间的数量关系为 .
(2)如图3,当但点E、F分别在线段BC、CD的延长线上时,其他条件不变,请探究线段BE、EF、FD之间的数量关系,并说明理由.
(二)拓展延伸
如图4,在等边△ABC中,E、F是边BC上的两点,∠EAF=30°,BE=1,将△ABE绕点A逆时针旋转60°得到△A′B′E′(A′B′与AC重合),连接EE′,AF与EE′交于点N,过点A作AM⊥BC于点M,连接MN,求线段MN的长度.
【答案】(一)(1)30,BE+DF=EF;(2)BE﹣DF=EF;(二)![]() .
.
【解析】
试题分析:(一)(1)根据图形旋转前后对应边相等,对应角相等,判定△AEF≌△AE′F,进而根据线段的和差关系得出结论;
(2)先在BE上截取BG=DF,连接AG,构造△ABG≌△ADF,进而利用全等三角形的对应边相等,对应角相等,判定△GAE≌△FAE,最后根据线段的和差关系得出结论;
(二)先根据旋转的性质判定△AEE′是等边三角形,进而利用等边△ABC、等边△AEE′的三线合一的性质,得到![]() 和∠BAE=∠MAN,最后判定△BAE∽△MAN,并根据相似三角形对应边成比例,列出比例式求得MN的长.
和∠BAE=∠MAN,最后判定△BAE∽△MAN,并根据相似三角形对应边成比例,列出比例式求得MN的长.
试题解析:(一)(1)如图2,将△ABE绕点A逆时针旋转60°后得到△A′B′E′,则
∠1=∠2,BE=DE′,AE=AE′,∵∠BAD=60°,∠EAF=30°,∴∠1+∠3=30°,∴∠2+∠3=30°,即∠FAE′=30°,∴∠EAF=∠FAE′,在△AEF和△AE′F中,∵AE=AE′,∠EAF=∠FAE′,AF=AF,∴△AEF≌△AE′F(SAS),∴EF=E′F,即EF=DF+DE′,∴EF=DF+BE,即线段BE、EF、FD之间的数量关系为BE+DF=EF,故答案为:30,BE+DF=EF;
(2)如图3,在BE上截取BG=DF,连接AG,在△ABG和△ADF中,∵AB=AD,∠ABE=∠ADF,BG=DF,∴△ABG≌△ADF(SAS),∴∠BAG=∠DAF,且AG=AF,∵∠DAF+∠DAE=30°,∴∠BAG+∠DAE=30°,∵∠BAD=60°,∴∠GAE=60°﹣30°=30°,∴∠GAE=∠FAE,在△GAE和△FAE中,∵AG=AF,∠GAE=∠FAE,AE=AE,∴△GAE≌△FAE(SAS),∴GE=FE,又∵BE﹣BG=GE,BG=DF,∴BE﹣DF=EF,即线段BE、EF、FD之间的数量关系为BE﹣DF=EF;
(二)如图4,将△ABE绕点A逆时针旋转60°得到△A′B′E′,则
AE=AE′,∠EAE′=60°,∴△AEE′是等边三角形,又∵∠EAF=30°,∴AN平分∠EAF,∴AN⊥EE′,∴直角三角形ANE中,![]() =
=![]() ,∵在等边△ABC中,AM⊥BC,∴∠BAM=30°,∴
,∵在等边△ABC中,AM⊥BC,∴∠BAM=30°,∴![]() =
=![]() ,且∠BAE+∠EAM=30°,∴
,且∠BAE+∠EAM=30°,∴![]() ,又∵∠MAN+∠EAM=30°,∴∠BAE=∠MAN,∴△BAE∽△MAN,∴
,又∵∠MAN+∠EAM=30°,∴∠BAE=∠MAN,∴△BAE∽△MAN,∴![]() ,即
,即![]() =
=![]() ,∴MN=
,∴MN=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】为了节约水资源,某市准备按照居民家庭年用水量实行阶梯水价.水价分档递增,计划使第一档、第二档和第三档的水价分别覆盖全市居民家庭的80%,15%和5%,为合理确定各档之间的界限,随机抽查了该市5万户居民家庭上一年的年用水量(单位:m3),绘制了统计图.如图所示,下面四个推断( )
①年用水量不超过180m3的该市居民家庭按第一档水价交费;
②年用水量超过240m3的该市居民家庭按第三档水价交费;
③该市居民家庭年用水量的中位数在150﹣180之间;
④该市居民家庭年用水量的平均数不超过180.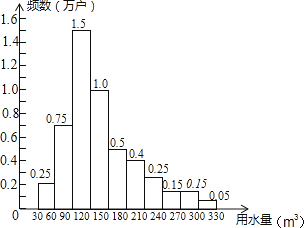
A.①③
B.①④
C.②③
D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,2,3分别以△ABC的AB和AC为边向△ABC外作正三角形(等边三角形)、正四边形(正方形)、正五边形,BE和CD相交于点O.
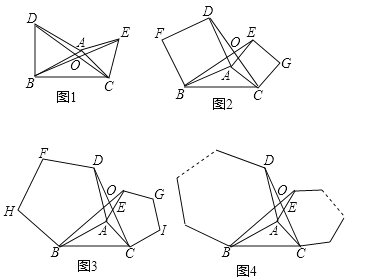
(1)在图1中,求证:△ABE≌△ADC.
(2)由(1)证得△ABE≌△ADC,由此可推得在图1中∠BOC=120°,请你探索在图2中,∠BOC的度数,并说明理由或写出证明过程.
(3)填空:在上述(1)(2)的基础上可得在图3中∠BOC= (填写度数).
(4)由此推广到一般情形(如图4),分别以△ABC的AB和AC为边向△ABC外作正n边形,BE和CD仍相交于点O,猜想得∠BOC的度数为 (用含n的式子表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com