练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】在平面直角坐标系中，已知两点A（1，2），B（﹣1，﹣1），若△ABC是以线段AB为一腰，对称轴平行于y轴的等腰三角形，则C点的坐标是 ．

    【答案】（3，﹣1）或（﹣3，2）
    【解析】解：分两种情况：①当A为顶角顶点时，根据题意得：等腰三角形的对称轴为x=1，∵点B的坐标为（﹣1，﹣1），∴点C的坐标为（3，﹣1）；②当B为顶角顶点时，根据题意得：等腰三角形的对称轴为x=﹣1，∵点A的坐标为（1，2），∴点C的坐标为（﹣3，2）；综上所述：C点的坐标为（3，﹣1）或（﹣3，2）；所以答案是：（3，﹣1）或（﹣3，2）．
    【考点精析】解答此题的关键在于理解等腰三角形的判定的相关知识，掌握如果一个三角形有两个角相等，那么这两个角所对的边也相等（简称：等角对等边）．这个判定定理常用于证明同一个三角形中的边相等．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

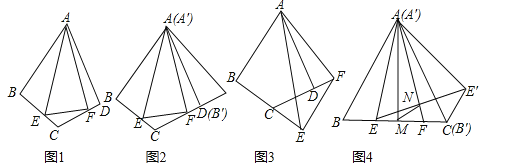
    【题目】在学习了图形的旋转知识后，数学兴趣小组的同学们又进一步对图形旋转前后的线段之间、角之间的关系进行了探究．

    （一）尝试探究

    如图1，在四边形ABCD中，AB=AD，∠BAD=60°，∠ABC=∠ADC=90°，点E、F分别在线段BC、CD上，∠EAF=30°，连接EF．

    （1）如图2，将△ABE绕点A逆时针旋转60°后得到△A′B′E′（A′B′与AD重合），请直接写出∠E′AF= 度，线段BE、EF、FD之间的数量关系为 ．

    （2）如图3，当但点E、F分别在线段BC、CD的延长线上时，其他条件不变，请探究线段BE、EF、FD之间的数量关系，并说明理由．

    （二）拓展延伸

    如图4，在等边△ABC中，E、F是边BC上的两点，∠EAF=30°，BE=1，将△ABE绕点A逆时针旋转60°得到△A′B′E′（A′B′与AC重合），连接EE′，AF与EE′交于点N，过点A作AM⊥BC于点M，连接MN，求线段MN的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】与 在平面直角坐标系中的位置如图.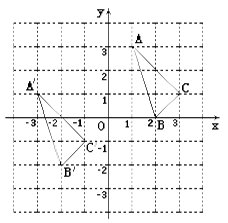

    （1）分别写出下列各点的坐标：
    ； ； ；
    （2）说明 由 经过怎样的平移得到:
    ．
    （3）若点 （ ， ）是 内部一点，则平移后 内的
    对应点 的坐标为；
    （4）求 的面积.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，l是四边形ABCD的对称轴，AD∥BC，现给出下列结论： ①AB∥CD；②AB=BC；③AB⊥BC；④AO=OC．其中正确的结论有（ ）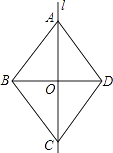

    A.1个
    B.2个
    C.3个
    D.4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正六边形ABCDEF关于直线l的轴对称图形是六边形A′B′C′D′E′F′，下列判断错误的是（ ）

    A.AB=A′B′
    B.BC∥B′C′
    C.直线l⊥BB′
    D.∠A′=120°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】把方程x2﹣4x+3＝0化为（x+m）2＝n形式，则m、n的值为（　　）

    A.2，1B.1，2C.﹣2，1D.﹣2，﹣1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知A，B两点在直线1的同侧，点A′与A关于直线l对称，连接A′B交l于点P．若A′B=a。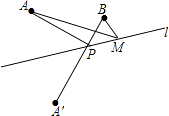

    （1）求AP+PB。
    （2）若点M是直线l上异于点P的任意一点，求证：AM+MB＞AP+PB。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为支援灾区，某校爱心活动小组准备用筹集的资金购买A、B两种型号的学习用品共1000件．已知B型学习用品的单价比A型学习用品的单价多10元，用180元购买B型学习用品的件数与用120元购买A型学习用品的件数相同．
    （1）求A、B两种学习用品的单价各是多少元？
    （2）若购买这批学习用品的费用不超过28000元，则最多购买B型学习用品多少件？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，D是BC边上的中点，∠BDE=∠CDF，请你添加一个条件，使DE=DF成立．你添加的条件是 ． （不再添加辅助线和字母）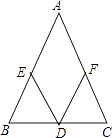

    查看答案和解析>>

    同步练习册答案