
【题目】如图所示,l是四边形ABCD的对称轴,AD∥BC,现给出下列结论: ①AB∥CD;②AB=BC;③AB⊥BC;④AO=OC.其中正确的结论有( )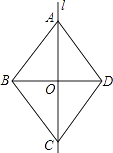
A.1个
B.2个
C.3个
D.4个
【答案】C
【解析】解:∵l是四边形ABCD的对称轴, ∴∠CAD=∠BAC,∠ACD=∠ACB,
∵AD∥BC,
∴∠CAD=∠ACB,
∴∠CAD=∠ACB=∠BAC=∠ACD,
∴AB∥CD,AB=BC,故①②正确;
又∵l是四边形ABCD的对称轴,
∴AB=AD,BC=CD,
∴AB=BC=CD=AD,
∴四边形ABCD是菱形,
∴AO=OC,故④正确,
∵菱形ABCD不一定是正方形,
∴AB⊥BC不成立,故③错误,
综上所述,正确的结论有①②④共3个.
故选C.
根据轴对称图形的性质,四边形ABCD沿直线l对折能够完全重合,再根据两直线平行,内错角相等可得∠CAD=∠ACB=∠BAC=∠ACD,然后根据内错角相等,两直线平行即可判定AB∥CD,根据等角对等边可得AB=BC,然后判定出四边形ABCD是菱形,根据菱形的对角线互相垂直平分即可判定AO=OC;只有四边形ABCD是正方形时,AB⊥BC才成立.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图1,2,3分别以△ABC的AB和AC为边向△ABC外作正三角形(等边三角形)、正四边形(正方形)、正五边形,BE和CD相交于点O.
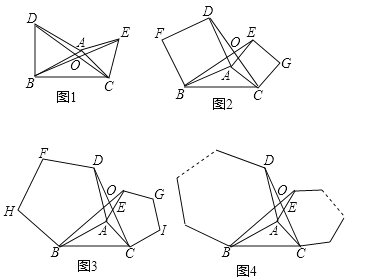
(1)在图1中,求证:△ABE≌△ADC.
(2)由(1)证得△ABE≌△ADC,由此可推得在图1中∠BOC=120°,请你探索在图2中,∠BOC的度数,并说明理由或写出证明过程.
(3)填空:在上述(1)(2)的基础上可得在图3中∠BOC= (填写度数).
(4)由此推广到一般情形(如图4),分别以△ABC的AB和AC为边向△ABC外作正n边形,BE和CD仍相交于点O,猜想得∠BOC的度数为 (用含n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠A=20°,若将△ABC沿CD折叠,使点B落在AC边上的点E处,则∠CED的度数是( ) 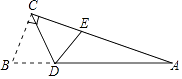
A.30°
B.40°
C.50°
D.70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究归纳题: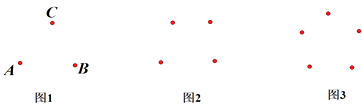
(1)试验分析:
如图1,经过A点与B、C两点分别作直线,可以作条;同样,经过B点与A、C两点分别作直线,可以作条;经过C点与A、B两点分别作直线,可以作条.
通过以上分析和总结,图1共有条直线.
(2)拓展延伸:
运用(1)的分析方法,可得:
图2共有条直线;
图3共有条直线;
(3)探索归纳:
如果平面上有n(n≥3)个点,且每3个点均不在同一直线上,经过其中两点共有条直线.(用含n的式子表示)
(4)解决问题:
中职篮(CBA)2017——2018赛季作出重大改革,比赛队伍数扩充为20支,截止2017年12月21日赛程过半,即每两队之间都赛了一场,请你帮助计算一下一共进行了多少场比赛?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星期六,小亮从家里骑自行车到同学家去玩,然后返回,图是他离家的路程y(千米)与时间x(分钟)的函数图象,根据图象信息,下列说法不一定正确的是( ) 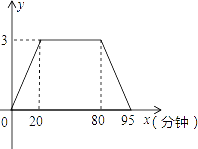
A.小亮到同学家的路程是3千米
B.小亮在同学家逗留的时间是1小时
C.小亮去时走上坡路,回家时走下坡路
D.小亮回家时用的时间比去时用的时间少
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1的解析式为y=﹣2x+2,且l1与x轴交于点D,直线l2经过点A(4,0),B(0,﹣1),两直线交于点C.
(1)点D的坐标为;
(2)求直线l2的表达式;
(3)求△ADC的面积;
(4)若有过点C的直线CE把△ADC的面积分为2:1两部分,请直接写出直线CE的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com