
【题目】三角形的下列四种线段中一定能将三角形分成面积相等的两部分的是( )
A.角平分线
B.中位线
C.高
D.中线
【答案】D
【解析】解:( 1 ) 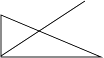 三角形的角平分线把三角形分成两部分,这两部分的面积比分情况而定;
三角形的角平分线把三角形分成两部分,这两部分的面积比分情况而定;
( 2 ) 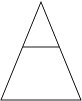
三角形的中位线把三角形分成两部分,这两部分的面积经计算得:
三角形面积为梯形面积的;
( 3 ) 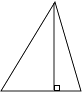
三角形的高把三角形分成两部分,这两部分的面积比分情况而定;
( 4 ) 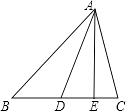
三角形的中线AD把三角形分成两部分,△ABD的面积为BDAE,△ACD面积为CDAE;因为AD为中线,所以D为BC中点,所以BD=CD,所以△ABD的面积等于△ACD的面积。
∴三角形的中线把三角形分成面积相等的两部分。
所以答案是:D。
【考点精析】解答此题的关键在于理解三角形的“三线”的相关知识,掌握1、三角形角平分线的三条角平分线交于一点(交点在三角形内部,是三角形内切圆的圆心,称为内心);2、三角形中线的三条中线线交于一点(交点在三角形内部,是三角形的几何中心,称为中心);3、三角形的高线是顶点到对边的距离;注意:三角形的中线和角平分线都在三角形内.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为-6,点B在数轴上A点右侧,则AB=14,动点M从点A出发,以每秒5个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>O)秒.![]()
(1)写出数轴上点B表示的数 , 点M表示的数 (用含t的式子表示).
(2)动点N从点B出发,以每秒3个单位长度的速度沿数轴向右匀速运动,若点M,N同时出发,问点M运动多少秒时追上点N?
(3)若P为AM的中点,F为MB的中点,点M在运动过程中,线段_PF的长度是否发生变化?若变化,请说明理由;若不变,请求出线段PF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校需要添置某种教学仪器,现有两种添置方法方案1:到厂商家购买,每件需要8元和一次性的运费2000元;方案2:学校自己制作,每件4元,另外购置制作工具的费用4200元,请问添置多少件这种教学仪器时两种方案所需费用恰好一样多.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠BAC=90°,过点B的直线MN∥AC,D为BC边上一点,连接AD,作DE⊥AD交MN于点E,连接AE.
(1)如图①,当∠ABC=45°时,求证:AD=DE;
(2)如图②,当∠ABC=30°时,线段AD与DE有何数量关系?并请说明理由;
(3)当∠ABC=α时,请直接写出线段AD与DE的数量关系.(用含α的三角函数表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
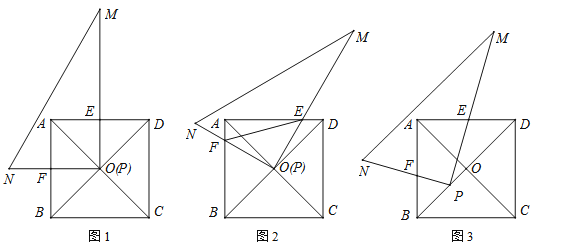
【题目】在正方形ABCD中,对角线AC与BD交于点O;在Rt△PMN中,∠MPN=90°.
(1)如图1,若点P与点O重合且PM⊥AD、PN⊥AB,分别交AD、AB于点E、F,请直接写出PE与PF的数量关系;
(2)将图1中的Rt△PMN绕点O顺时针旋转角度α(0°<α<45°).
①如图2,在旋转过程中(1)中的结论依然成立吗?若成立,请证明;若不成立,请说明理由;
②如图2,在旋转过程中,当∠DOM=15°时,连接EF,若正方形的边长为2,请直接写出线段EF的长;
③如图3,旋转后,若Rt△PMN的顶点P在线段OB上移动(不与点O、B重合),当BD=3BP时,猜想此时PE与PF的数量关系,并给出证明;当BD=mBP时,请直接写出PE与PF的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
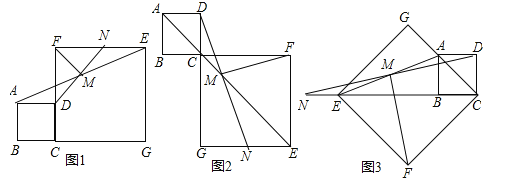
【题目】如图1所示,在正方形ABCD和正方形CGEF中,点B、C、G在同一条直线上,M是线段AE的中点,DM的延长线交EF于点N,连接FM,易证:DM=FM,DM⊥FM(无需写证明过程)
(1)如图2,当点B、C、F在同一条直线上,DM的延长线交EG于点N,其余条件不变,试探究线段DM与FM有怎样的关系?请写出猜想,并给予证明;
(2)如图3,当点E、B、C在同一条直线上,DM的延长线交CE的延长线于点N,其余条件不变,探究线段DM与FM有怎样的关系?请直接写出猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第一次模拟试后,数学科陈老师把一班的数学成绩制成如图的统计图,并给了几个信息:①前两组的频率和是0.14;②第一组的频率是0.02;③自左到右第二、三、四组的频数比为3:9:8,然后布置学生(也请你一起)结合统计图完成下列问题: 
(1)全班学生是多少人?
(2)成绩不少于90分为优秀,那么全班成绩的优秀率是多少?
(3)若不少于100分可以得到A+等级,则小明得到A+的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习了图形的旋转知识后,数学兴趣小组的同学们又进一步对图形旋转前后的线段之间、角之间的关系进行了探究.
(一)尝试探究
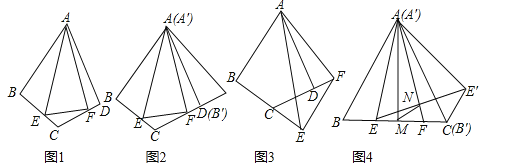
如图1,在四边形ABCD中,AB=AD,∠BAD=60°,∠ABC=∠ADC=90°,点E、F分别在线段BC、CD上,∠EAF=30°,连接EF.
(1)如图2,将△ABE绕点A逆时针旋转60°后得到△A′B′E′(A′B′与AD重合),请直接写出∠E′AF= 度,线段BE、EF、FD之间的数量关系为 .
(2)如图3,当但点E、F分别在线段BC、CD的延长线上时,其他条件不变,请探究线段BE、EF、FD之间的数量关系,并说明理由.
(二)拓展延伸
如图4,在等边△ABC中,E、F是边BC上的两点,∠EAF=30°,BE=1,将△ABE绕点A逆时针旋转60°得到△A′B′E′(A′B′与AC重合),连接EE′,AF与EE′交于点N,过点A作AM⊥BC于点M,连接MN,求线段MN的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】与 ![]() 在平
在平![]() 面直角坐标系中的位置如图.
面直角坐标系中的位置如图.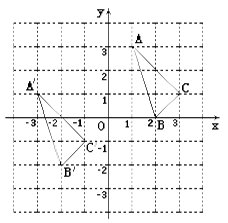
(1)分别写出下列各点的坐标:![]() ;
; ![]() ;
; ![]() ;
;
(2)说明 ![]() 由
由 ![]() 经过怎样的平移得到:
经过怎样的平移得到:
.
(3)若点 ![]() (
( ![]() ,
, ![]() )是
)是 ![]() 内部一点,则平移后
内部一点,则平移后 ![]() 内的
内的
对应点 ![]() 的坐标为;
的坐标为;
(4)求 ![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com