
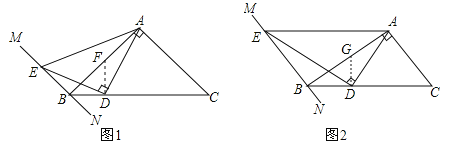
【题目】在Rt△ABC中,∠BAC=90°,过点B的直线MN∥AC,D为BC边上一点,连接AD,作DE⊥AD交MN于点E,连接AE.
(1)如图①,当∠ABC=45°时,求证:AD=DE;
(2)如图②,当∠ABC=30°时,线段AD与DE有何数量关系?并请说明理由;
(3)当∠ABC=α时,请直接写出线段AD与DE的数量关系.(用含α的三角函数表示)

【答案】(1)证明见试题解析;(2)DE=![]() AD;(3)AD=DEtanα.
AD;(3)AD=DEtanα.
【解析】
试题分析:(1)过点D作DF⊥BC,交AB于点F,得出∠BDE=∠ADF,∠EBD=∠AFD,即可得到△BDE≌△FDA,从而得到AD=DE;
(2)过点D作DG⊥BC,交AB于点G,进而得出∠EBD=∠AGD,证出△BDE∽△GDA即可得出答案;
(3)过点D作DG⊥BC,交AB于点G,进而得出∠EBD=∠AGD,证出△BDE∽△GDA即可得出答案.
试题解析:(1)如图1,过点D作DF⊥BC,交AB于点F,则∠BDE+∠FDE=90°,∵DE⊥AD,∴∠FDE+∠ADF=90°,∴∠BDE=∠ADF,∵∠BAC=90°,∠ABC=45°,∴∠C=45°,∵MN∥AC,∴∠EBD=180°﹣∠C=135°,∵∠BFD=45°,DF⊥BC,∴∠BFD=45°,BD=DF,∴∠AFD=135°,∴∠EBD=∠AFD,在△BDE和△FDA中,∵∠EBD=∠AFD,BD=DF,∠BDF=∠ADF,∴△BDE≌△FDA(ASA),∴AD=DE;
(2)DE=![]() AD,理由:
AD,理由:
如图2,过点D作DG⊥BC,交AB于点G,则∠BDE+∠GDE=90°,∵DE⊥AD,∴∠GDE+∠ADG=90°,∴∠BDE=∠ADG,∵∠BAC=90°,∠ABC=30°,∴∠C=60°,∵MN∥AC,∴∠EBD=180°﹣∠C=120°,∵∠ABC=30°,DG⊥BC,∴∠BGD=60°,∴∠AGD=120°,∴∠EBD=∠AGD,∴△BDE∽△GDA,∴![]() ,在Rt△BDG中,
,在Rt△BDG中,![]() =tan30°=
=tan30°=![]() ,∴DE=
,∴DE=![]() AD;
AD;
(3)AD=DEtanα;理由:
如图2,∠BDE+∠GDE=90°,∵DE⊥AD,∴∠GDE+∠ADG=90°,∴∠BDE=∠ADG,∵∠EBD=90°+α,∠AGD=90°+α,∴∠EBD=∠AGD,∴△EBD∽△AGD,∴![]() ,在Rt△BDG中,
,在Rt△BDG中,![]() =tanα,则
=tanα,则![]() =tanα,∴AD=DEtanα.
=tanα,∴AD=DEtanα.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】为了节约水资源,某市准备按照居民家庭年用水量实行阶梯水价.水价分档递增,计划使第一档、第二档和第三档的水价分别覆盖全市居民家庭的80%,15%和5%,为合理确定各档之间的界限,随机抽查了该市5万户居民家庭上一年的年用水量(单位:m3),绘制了统计图.如图所示,下面四个推断( )
①年用水量不超过180m3的该市居民家庭按第一档水价交费;
②年用水量超过240m3的该市居民家庭按第三档水价交费;
③该市居民家庭年用水量的中位数在150﹣180之间;
④该市居民家庭年用水量的平均数不超过180.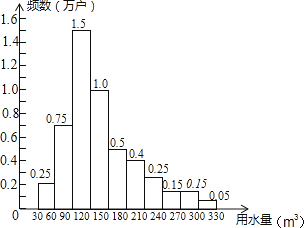
A.①③
B.①④
C.②③
D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第一次模拟试后,数学科陈老师把一班的数学成绩制成如图的统计图,并给了几个信息:①前两组的频率和是0.14;②第一组的频率是0.02;③自左到右第二、三、四组的频数比为3:9:8,然后布置学生(也请你一起)结合统计图完成下列问题: 
(1)全班学生是多少人?
(2)成绩不少于90分为优秀,那么全班成绩的优秀率是多少?
(3)若不少于100分可以得到A+等级,则小明得到A+的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2013年四川泸州2分)下列各式计算正确的是【 】
A.(a7)2=a9 B.a7a2=a14 C.2a2+3a3=5a5 D.(ab)3=a3b3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,2,3分别以△ABC的AB和AC为边向△ABC外作正三角形(等边三角形)、正四边形(正方形)、正五边形,BE和CD相交于点O.
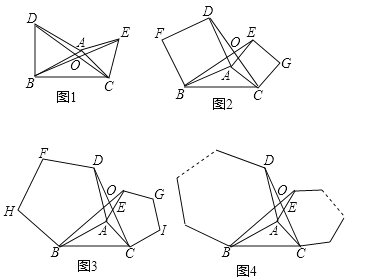
(1)在图1中,求证:△ABE≌△ADC.
(2)由(1)证得△ABE≌△ADC,由此可推得在图1中∠BOC=120°,请你探索在图2中,∠BOC的度数,并说明理由或写出证明过程.
(3)填空:在上述(1)(2)的基础上可得在图3中∠BOC= (填写度数).
(4)由此推广到一般情形(如图4),分别以△ABC的AB和AC为边向△ABC外作正n边形,BE和CD仍相交于点O,猜想得∠BOC的度数为 (用含n的式子表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com