
已知AB是半圆O的直径,点C是半圆O上的动点,点D是线段AB延长线上的动点,在运动过程中,保持CD=OA.
(1)当直线CD与 半圆O相切时(如图①),求∠ODC的度数;
半圆O相切时(如图①),求∠ODC的度数;
(2)当直线CD与半圆O相交时(如 图②),设另一交点为E,连接AE,若AE∥OC,
图②),设另一交点为E,连接AE,若AE∥OC,
①AE与OD的大小有什么关系? 为什么?
为什么?
②求∠ODC的度数.
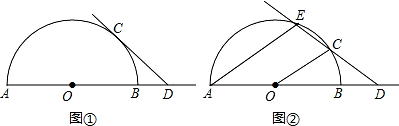
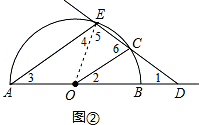
解:(1)如图①,连接OC,
∵OC=OA,CD=OA,
∴OC=CD,
∴∠ODC=∠COD,
∵CD是⊙O的切线,
∴∠OCD=90°,
∴∠ODC=45° ;
;
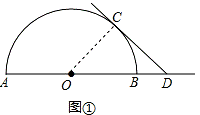
(2)如图②,连接OE.
∵CD=OA,∴CD=OC=OE=OA,
∴∠1=∠2,∠3=∠4.
∵AE∥OC,
∴∠2=∠3.
设∠ODC=∠1=x,则∠2=∠3=∠4=x.
∴∠AOE=∠OCD=180°﹣2x.
①AE=OD.理由如下:
在△AOE与△OCD中,
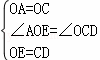
∴△AOE≌△OCD(SAS),
∴AE=OD.
②∠6=∠1+∠2=2x.
∵OE=OC,∴∠5=∠6=2x.
∵AE∥OC,
∴∠4+∠5 +∠6=180°,即:x+2x+2x=180°,
+∠6=180°,即:x+2x+2x=180°,
∴x=36°.
∴∠ODC=36°.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
下列命题:①圆心不同,直径相等的两圆是等圆;②长度相等的两弧是等弧;③圆中最长的弦是直径;④圆的对称轴是圆的直径;⑤圆不是旋转对称图形 .其中正确的有( )
.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
个钢管放在V形架内,右图是其截面图,O为钢管的圆心.如果钢管的半径为25 cm,∠MPN 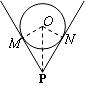 = 60°,则
= 60°,则 OP =( )
OP =( )
A.50 cm B.25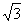 cm
cm
C.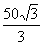 cm D.50
cm D.50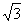 cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
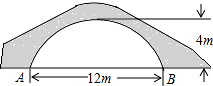
如图的一座拱桥,当水面宽AB为12m时,桥洞顶部离水面4m,已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点时的抛物线解析式是y=﹣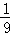 (x﹣6)2+4,则选取点B为坐标原点时的抛物线解析式是 .
(x﹣6)2+4,则选取点B为坐标原点时的抛物线解析式是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com