试题分析:(1)连接AC,则AC必过O点,延长FO交AB于M,由于O是BD中点,易证得△AOM≌△FOE,则AO=EF.
(2)方法与①类似,延长FP交AB于M,延长AP交BC于N,易证得四边形MBEP是正方形,可证得△APM≌△FEP,则AP=EF.
(3)解题思路和方法同(2).
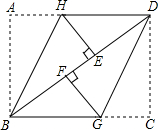
试题解析:(1)如图1,

证明:连接AC,则AC必过点O,
∵四边形ABCD是正方形,AC是对角线.
∵OF⊥CD,FOM共线,
∵OM⊥AB,OE⊥BC.
∴∠ABE=∠BEO=∠BMO=90°
∴四边形OEBM是矩形.
∵AC平分∠BCD且OE⊥BC,OF⊥CD,
∴OF= OE
∴矩形OECF是正方形
∴∠MAO=∠OFE=∠AOM=∠OEF=45°,∠AMO=∠EOF=90°,
∴OM=OE=OF=AM
∴△AMO≌△FOE(AAS),
∴AP=EF.
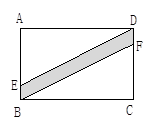
(2)如图2,

∵PM⊥AB,PE⊥BC,∠MBE=90°,且∠MBP=∠EBP=45°,
∴四边形MBEP是正方形,
∴MP=PE,∠AMP=∠FPE=90°;
又∵AB﹣BM=AM,BC﹣BE=EC=PF,
且AB=BC,BM=BE,
∴AM=PF,
∴△AMP≌△FPE(SAS),
∴AP=EF.
(3)AP=EF,且AP⊥EF.